- how to construct 1300with the help of a compass?
- how to construct 1350with the help of a compass?
- how to construct 950with the help of a compass?
- how to construct 850with the help of a compass?
- how to construct 800with the help of a compass?
- how to construct 1500with the help of a compass?
@All : Good attempt. Keep it up!
@Rohit Narain : Good to know that your got your answer.
- 1
It is not possible.
This page:
http://myyn.org/m/article/constructible-…
proves that the only constructable angles with integer numbers
of degrees are those whose measure is a multiple of 3 degrees.
130, 95, 85, 80, are not such a number.
- 0
85 Degree Angle – Using Protractor:
To measure the Angle:

To Make The Angle – 52 Degree:

Procedure for the 85 degree angle:
Step 1: Draw the reference line as AB.
Step 2: Place the protractor hole (center of the protractor) over the vertex on the point A of the reference line AB.
Step 3: Now refer the angle from 0 degree to 85 degree as from right side.
Step 4: Mark the point as C and the joint the point to the point A which make the angle 85 degree as acute angle.
By using the straight edge of the protractor to join the mark to the end point of the reference line AB, forming an angle ABC is 85 degree.
The below given steps will be followed to construct an angle of 135�.
(1) Draw a line l and mark a point P on it. Now taking P as centre and with a convenient radius, draw a semi-circle which intersects line l at Q and R.
(2) Taking R as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at S.
(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T (see figure).
(4) Taking S and T as centre, draw arcs of same radius to intersect each other at U.
(5) Join PU. Let it intersect the arc at V. Now taking Q and V as centres and with radius more than ![]() QV, draw arcs to intersect each other at W.
QV, draw arcs to intersect each other at W.
(6) Join PW which is the required ray making 135� with line l.

1689589.png)
Construction steps:
1. Draw a line AB.
2. Take a point P on it.
3. Draw an arc from point P to cut AB at C and D.
4. Now, take CP as radius, draw two arcs from points C and D. Intersection of these two arcs gives an angle of 90�.
5. Draw an arc from point P on the left side of x - axis to cut it at point Q.
6. Now, take PM as radius, draw an arc from Point Q to cut the previous arc at a point E.
7. Join PE. ∠NPE = 60�
8. ∠EPB = ∠NPE + ∠BPN = 90� + 60� = 150�.
If you are satisfied do give thumbs up.
- 2
1. Construction of an Angle of 60° by using Compass
Step of Construction:
(i) Draw a ray OA.
(ii) With O as centre and any suitable radius draw an arc above OA cutting it at a point B.
(iii) With B as centre and the same radius as before, draw another arc to cut the previous arc at C.
(iv) Join OC and produce it to D.

Then ∠AOD = 60°.
2. Construction of an Angle of 120° by using Compass
Step of Construction:
(i) Draw a ray OA.
(ii) With O as centre and any suitable radius draw an arc cutting OA at B.
(iii) With B as centre and the same radius cut the arc at C, then with C as centre and same radius cut the arc at D. Join OD and produce it to E.

Then, ∠AOE = 120°.
3. Construction of an Angle of 30° by using Compass
Step of Construction:
(i) Construction an angle ∠AOD = 60° as shown.
(ii) Draw the bisector OE of ∠AOD.

Then, ∠AOD = 30°.
4. Construction of an Angle of 90° by using Compass
Step of Construction:
(i) Take any ray OA.
(ii) With O as centre and any convenient radius, draw an arc cutting OA at B.
(iii) With B as centre and the same radius, draw an cutting the first arc at C.
(iv) With C as centre and the same radius, cut off an arc cutting again the first arc at D.
(v) With C and D as centre and radius of more than half of CD, draw two arcs cutting each other at E, join OE.

Then, ∠EOA = 90°.
5. Construction of an Angle of 75° by using Compass
Step of Construction:
(i) Take a ray OA.
(ii) With O as centre and any convenient radius, draw an arc cutting OA at C.
(iii) With C as centre and the same radius, draw an cutting the first arc at M.
(iv) With M as centre and the same radius, cut off an arc cutting again the first arc at L.
(v) With L and M as centre and radius of more than half of LM, draw two arcs cutting each other at B, join OB which is making 90°.
(vi) Now with N and M as centres again draw two arcs cutting each other at P.
(vii) Join OP.

Then, ∠POA = 75°.
6. Construction of an Angle of 105° by using Compass
Step of Construction:
(i) After making 90° angle take L and N as centre and draw two arcs cutting each other at S.
(ii) Join SO.

Then, ∠SOA = 105°.
7. Construction of an Angle of 135° by using Compass
Step of Construction:
(i) Construct ∠AOD = 90°
(ii) Produce ∠AO to B.
(iii) Draw OE to bisect ∠DOB.
∠DOE = 45°
∠EOA = 45° + 90° = 135°

Then, ∠EOA = 135°.
8. Construction of an Angle of 150° by using Compass
Step of Construction:
(i) Construct ∠AOC = 120°
(ii) Produce ∠AO to B.
(iii) Draw OD to bisect ∠COB.
Now ∠COD = 30°
Therefore, ∠AOD = 120° + 30° = 150°

Then, ∠AOD = 150°.
- 2
1. Construction of an Angle of 60° by using Compass
Step of Construction:
(i) Draw a ray OA.
(ii) With O as centre and any suitable radius draw an arc above OA cutting it at a point B.
(iii) With B as centre and the same radius as before, draw another arc to cut the previous arc at C.
(iv) Join OC and produce it to D.
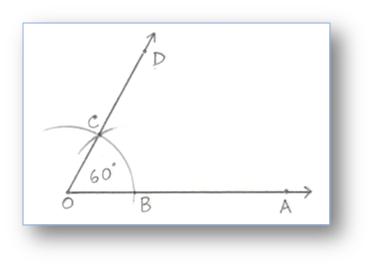
Then ∠AOD = 60°.
2. Construction of an Angle of 120° by using Compass
Step of Construction:
(i) Draw a ray OA.
(ii) With O as centre and any suitable radius draw an arc cutting OA at B.
(iii) With B as centre and the same radius cut the arc at C, then with C as centre and same radius cut the arc at D. Join OD and produce it to E.
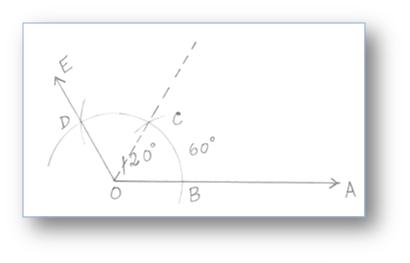
Then, ∠AOE = 120°.
3. Construction of an Angle of 30° by using Compass
Step of Construction:
(i) Construction an angle ∠AOD = 60° as shown.
(ii) Draw the bisector OE of ∠AOD.
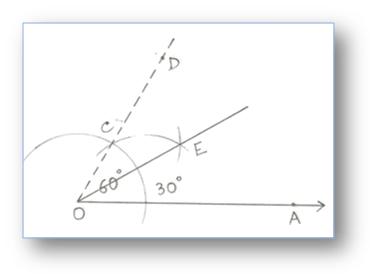
Then, ∠AOD = 30°.
4. Construction of an Angle of 90° by using Compass
Step of Construction:
(i) Take any ray OA.
(ii) With O as centre and any convenient radius, draw an arc cutting OA at B.
(iii) With B as centre and the same radius, draw an cutting the first arc at C.
(iv) With C as centre and the same radius, cut off an arc cutting again the first arc at D.
(v) With C and D as centre and radius of more than half of CD, draw two arcs cutting each other at E, join OE.
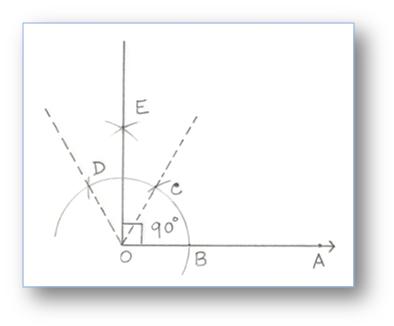
Then, ∠EOA = 90°.
5. Construction of an Angle of 75° by using Compass
Step of Construction:
(i) Take a ray OA.
(ii) With O as centre and any convenient radius, draw an arc cutting OA at C.
(iii) With C as centre and the same radius, draw an cutting the first arc at M.
(iv) With M as centre and the same radius, cut off an arc cutting again the first arc at L.
(v) With L and M as centre and radius of more than half of LM, draw two arcs cutting each other at B, join OB which is making 90°.
(vi) Now with N and M as centres again draw two arcs cutting each other at P.
(vii) Join OP.
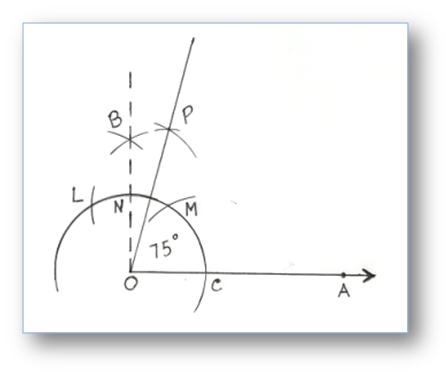
Then, ∠POA = 75°.
6. Construction of an Angle of 105° by using Compass
Step of Construction:
(i) After making 90° angle take L and N as centre and draw two arcs cutting each other at S.
(ii) Join SO.
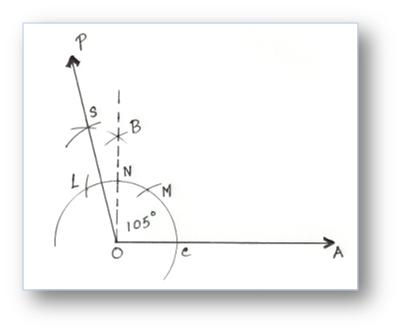
Then, ∠SOA = 105°.
7. Construction of an Angle of 135° by using Compass
Step of Construction:
(i) Construct ∠AOD = 90°
(ii) Produce ∠AO to B.
(iii) Draw OE to bisect ∠DOB.
∠DOE = 45°
∠EOA = 45° + 90° = 135°
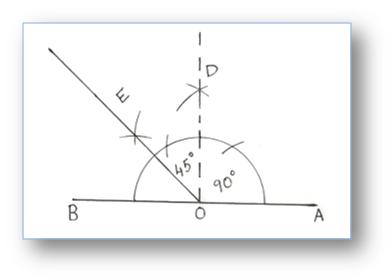
Then, ∠EOA = 135°.
8. Construction of an Angle of 150° by using Compass
Step of Construction:
(i) Construct ∠AOC = 120°
(ii) Produce ∠AO to B.
(iii) Draw OD to bisect ∠COB.
Now ∠COD = 30°
Therefore, ∠AOD = 120° + 30° = 150°
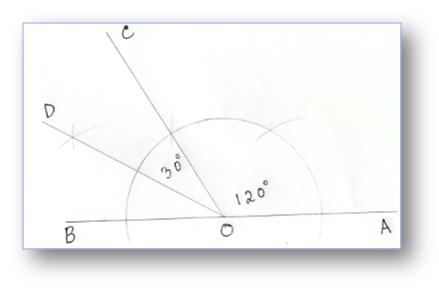
Then, ∠AOD = 150°.
The rest of the angles cannot be constructed by using compass.
- 1

