How to derive the formula for voulume of frustum of a cone?
- How to derive the relation bnetween the orginal cone radius / height to the portion of the cone that is removed?
The volume of a conical or pyramidal frustum is the volume of the solid before slicing the apex off, minus the volume of the apex:
where B1 is the area of one base, B2 is the area of the other base, and h1, h2 are the perpendicular heights from the apex to the planes of the two bases.
Considering that
the volume can also be expressed as the product of the height h = h2−h1 of the frustum, and the Heronian mean of their areas:
Heron of Alexandria is noted for deriving this formula and with it encountering the imaginary no, the square root of negative one.
In particular, the volume of a circular cone frustum is
where π is 3.14159265..., and R1, R2 are the radii of the two bases.
The volume of a pyramidal frustum whose bases are n-sided polygons is
where a1 and a2 are the sides of the two bases.
Surface area
The surface area of a right circular cone frustum is
where R1 and R2 are the base and top radii respectively.
The surface area of a right frustum whose bases are similar regular n-sided polygon is
where a1 and a2 are the sides of the two bases.


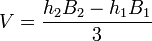

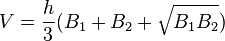



![A= pileft[(R_1^2+R_2^2)+sqrt{(R_1^2-R_2^2)^2+(h(R_1+R_2))^2}right]](http://upload.wikimedia.org/math/4/5/4/454d0c97b69b4c8f6636813b14505cef.png)
![A= frac{n}{4}left[(a_1^2+a_2^2)cot frac{pi}{n} + sqrt{(a_1^2-a_2^2)^2sec^2 frac{pi}{n}+4 h^2(a_1+a_2)^2} right]](http://upload.wikimedia.org/math/6/a/0/6a069b007cc4b8905f1e0e76219c70d4.png)









