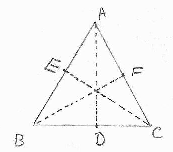
If the altitudes of a triangle ABC are equal,then prove that triangle is equilateral - Maths - Triangles

Question

If the altitudes of a triangle ABC are equal,then prove that
triangle is equilateral

Ankush Jain · Accepted Answer

Given, AD, BE and CF are the attitudes drawn on sides BC, CA and AB of Δ ABC such that AD = BE = CF

Area of Δ ABC = $\frac{1}{2}$ × BC × AD = $\frac{1}{2}$ × AB × CF = $\frac{1}{2}$ × CA × BE ( $∵$ Area of Δ = $\frac{1}{2}$ × Base × Correspondence attitude)

∴ BC × AD = AB × CF = CA × BE

⇒ BC = AB = CA ( $∵$ AD = BE = CF)

Hence, ΔABC is an equilateral triangle.

61

Steps	Statement	Reason
1	Consider triangles BEC and BFC
2	EC=BF	Equal altitudes(given)
3	BEC=BFC = 90⁰	BE and BF are Altitudes
4	BC is common
5	BEC BFC	RHS postulate
6	ABC = BCA	Corresponding angles
7	Consider the ADB and ADC
8	ADB=ADC = 90⁰	AD is Altitude
9	AD is common
10	ABC = BCA	Step 6
11	ADB ADC	ASA postulate
12	AB =AC	Corresponding sides are equal
13	BC= AC	Similarly we can prove BFC BFA
14	AB=AC=BC	Step 12,13

If the altitudes of a triangle ABC are equal,then prove that triangle is equilateral.