State and prove Gauss Theorem .
Gauss's law can be derived from Coulomb's law, which states that the electric field due to a stationary point charge is: where Using the expression from Coulomb's law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give where ρ is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem[5]Deriving Gauss's law from Coulomb's law
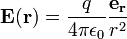
 is the electric constant,
is the electric constant,

