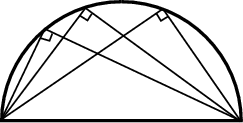
Well there can be several equations of legs of a right triangle with fixed hypotneuse. Let the perpendicular sides meet at B(x,y). Clearly this point lies on a circle whose diameter is the given hypotneuse.
(Property of chords of circle: Angle subtended by diameter at the circumference is 90 .)
We can find the locus of all those points where the perpendicular sides(legs) intersect. It will be an equation of circle. If we know the extremities of diameter, we can find the equation of circle by the following equation.
(x - x1)(x - x2) + (y - y1)(y - y2) = 0
(x - 1)(x + 4) + (y - 3)(y - 1) = 0
---
I am not multiplying them, because i see four solutions of the above equation.
x = 1, y = 1
x = 1, y = 3
x = -4, y = 1
x = -4, y = 3
-----
We can't take (1,3) and (-4, 1) because they are points A and C themselves. So solutions (1,1) and (-4, 3) will yeild two pairs of equations.
----
Let's take (1,1)
∴ Equation of line segment AB passing through points (1, 3) and (1, 1) is given by
, 
⇒ x 1 = 0
⇒ x = 1.
Equation of line segment BC passing through points (1, 1) and (4, 1) is given by,

⇒ y 1 = 0
⇒ y = 1
∴ Equations of legs of the triangle are x = 1 and y = 1.
-----
Similarly if you take B(x,y) = (-4,3)
slope of AB = (3 - 3)/(1 + 4) = 0
(y - 3) / ( x - 1) = slope = 0
y - 3 = 0
y = 3
---
slope of BC = (3 - 1)/(-4 + 4) = 1/0
(y - 1) / (x + 4) = slope = 1/0
x + 4 = 0
x = -4
You get equations of legs of triangle x = -4 and y = 3
