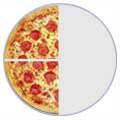
The best way to think about equivalent fractions is that they are fractions that have the same overall value. Equivalent fractions represent the same part of a whole.  For example, if we cut a pie exactly down the middle, into two equally sized pieces, one piece is the same as one half of the pie.

And if another pie (the same size) is cut into 4 equal pieces, then two pieces of that pie represent the same amount of pie that 1/2 did. So we can say that 1/2 is equivalent (or equal) to 2/4.

Don’t be confused!

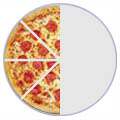
Take a look at the four circles above. Can you see that the one “1/2″, the two “1/4″ and the four “1/8″ take up the same amount of area colored in orange for their circle? Well that means that each area colored in orange is an equivalent fraction or equal amount. Therefore, we can say that 1/2 is equal to 2/4, and 1/2 is also equal to 4/8.

And yes grasshopper, 2/4 is an equivalent fraction for 4/8 too.

As you already know, we are nuts about rules. So, let’s look at the Rule to check to see if two fractions are equivalent or equal. The rule for equivalent fractions can be a little tough to explain, but hang in there, we will clear things up in just a bit.

Here’s the Rule…

What this Rule says is that two fractions are equivalent (equal) only if the product of the numerator (a) of the first fraction and the denominator (d) of the other fraction is equal to the product of the denominator (b) of the first fraction and the numerator (c) of the other fraction. A product simply means you multiply.

That sounds like a mouthful, so let’s try it with numbers…

Now let’s plug the numbers into the Rule for equivalent fractions to be sure you have it down “cold”.

3/4 is equivalent (equal) to 9/12 only if the product of the numerator (3) of the first fraction and the denominator (12) of the other fraction is equal to the product of the denominator (4) of the first fraction and the numerator (9) of the other fraction. So we know that 3/4 is equivalent to 9/12, because 3×12=36 and 4×9=36.

A simple way to look at how to check for equivalent fractions is to do what is called “cross-multiply”, which means multiple the numerator of one fraction by the denominator of the other fraction. Then do the same thing in reverse. Now compare the two answers to see if they are equal. If they are equal, then the two fractions are equivalent fractions.

The graphic below shows you how to cross multiply…

Okay, let’s do one with numbers where the fractions are not equivalent…

So you can see by this example, 1/2 is not an equivalent fraction of 2/3. If you remember to use the cross-multiply method, you should not have any problems verifying equivalent fractions.

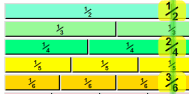
The table below lists some common fractions and their equivalents. Just read the table from left-to-right. What it shows you are values multiplied by different variations of fractions equal to “1″. You do remember that any number divided by itself is equal to “1″ right? For example…

Fractions equivalent to 1/2 are 2/4, 3/6, 4/8, 5/10, 6/12, …

Fractions equivalent to 1/5 are 2/10, 3/15, 4/20, 5/25, …

Equivalent Fractions Table

As you can see, knowing about equivalent fractions shows you that all fractions are not equivalent fractions.