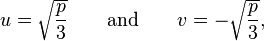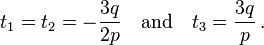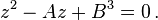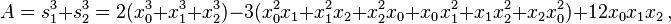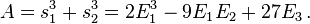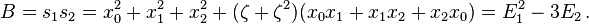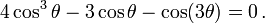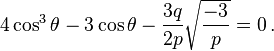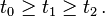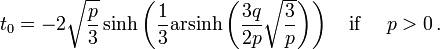What are the difinitions of linear, quadratic and cubic polynomials?
A polynomial of degree two is called a quadratic polynomial. It is of the form ax2 + bx + c. where a, b, c are real numbers and a≠ 0 Examples:x2-2x+5, x2-3x etc.
Again, a polynomial of degree three is called a cubic polynomial. It is of the form ax3 + bx2 + cx + d, where a, b, c, d are real numbers and a≠ 0 Examples: x3 + 8x2 -5x + 17, x3+ 9x + 6, etc.
- 0
The word linear comes from the Latin word linearis, which means created by lines. In mathematics, a linear map or function f(x) is a function which satisfies the following two properties:
- Additivity (also called the superposition property): f(x + y) = f(x) + f(y). This says that f is a group homomorphism with respect to addition.
- Homogeneity of degree 1: f(αx) = αf(x) for all α.
In a different usage to the above, a polynomial of degree 1 is said to be linear, because the graph of a function of that form is a line.
Over the reals, a linear equation is one of the form:
where m is often called the slope or gradient; b the y-intercept, which gives the point of intersection between the graph of the function and the y-axis.
Note that this usage of the term linear is not the same as the above, because linear polynomials over the real numbers do not in general satisfy either additivity or homogeneity. In fact, they do so if and only if b = 0. Hence, if b ≠ 0, the function is often called an affine function (see in greater generality affine transformation).
Hope it works...for u,
Cheerz....Plz thumbz up!
- -1
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2. For example, x2 − 4x + 7 is a quadratic polynomial, while x3 − 4x + 7 is not.
A quadratic polynomial may involve a single variable x, or multiple variables such as x, y, and z.
[edit] The one-variable case
Any single-variable quadratic polynomial may be written as
where x is the variable, and a, b, and c represent the coefficients. In elementary algebra, such polynomials often arise in the form of a quadratic equation ax2 + bx + c = 0. The solutions to this equation are called the roots of the quadratic polynomial, and may be found through factorization, completing the square, graphing, Newton's method, or through the use of the quadratic formula. Each quadratic polynomial has an associated quadratic function, whose graph is a parabola.
If the polynomial is a polynomial in one variable, it determines a quadratic function in one variable. An example is given by f(x) = x2 + x − 2;. The graph of such a function is a parabola (in degenerate cases a line), and its zeroes can be found by solving the quadratic equation f(x) = 0.
There are three main forms :
- general form,
 .
. - logistic form,
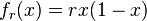 , used to study 1D discrete dynamics,
, used to study 1D discrete dynamics, - monic and centered form,
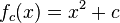 , used to study complex dynamics.
, used to study complex dynamics.
[edit] Two variables case
Any quadratic polynomial with two variables may be written as
where x and y are the variables and a, b, c, d, e, and f are the coefficients. Such polynomials are fundamental to the study of conic sections. Similarly, quadratic polynomials with three or more variables correspond to quadric surfaces and hypersurfaces. In linear algebra, quadratic polynomials can be generalized to the notion of a quadratic form on a vector space.
[edit] N variables case
In the general case, a quadratic polynomial in n variables x1, ..., xn can be written in the form
where Q is a symmetric n-dimensional matrix, P is an n-dimensional vector, and R a constant.
The coefficients of a polynomial are often taken to be real or complex numbers, but in fact, a polynomial may be defined over any ring.
When using the term "quadratic polynomial", authors sometimes mean "having degree exactly 2", and sometimes "having degree at most 2". If the degree is less than 2, this may be called a "degenerate case". Usually the context will establish which of the two is meant.
So
- This article discusses cubic equations in one variable. For a discussion of cubic equations in two variables, see elliptic curve.

In mathematics, a cubic function is a function of the form
where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function. The integral of a cubic function is a quartic function.
Setting ƒ(x) = 0 and assuming a ≠ 0 produces a cubic equation of the form:
Usually, the coefficients a, b,c, d are real numbers. However, most of the theory is also valid if they belong to a field of characteristic other than 2 or 3. Solving a cubic equation amounts to finding the roots or zeros of a cubic function. There are two ways to solve a cubic equation. One way is to express the roots as formulas involving simple functions like square and cube roots. This is the approach which is described in this page. Another way is to use a numerical approximation of the roots in the field of the real or complex numbers. This may be obtained by any root-finding algorithm, like Newton's method.
metimes the word "order" is used with the meaning of "degree", e.g. a second-order polynomial.Through the quadratic formula the roots of the derivative f′(x) = 3ax2 + 2bx + c are given by
and provide the critical points where the slope of the cubic function is zero. If b2 − 3ac > 0, then the cubic function has a local maximum and a local minimum. If b2 − 3ac = 0, then the cubic's inflection point is the only critical point. If b2 − 3ac > 0, then there are no critical points. In the cases where b2 − 3ac ≤ 0, the cubic function is strictly monotonic.
The general cubic equation has the form
with 
This section describes how the roots of such an equation may be computed. The coefficients a, b, c, d are generally assumed to be real numbers, but most of the results apply when they belong to any field of characteristic different of two and three.
[edit] The nature of the roots
Every cubic equation (1) with real coefficients has at least one solution x among the real numbers; this is a consequence of the intermediate value theorem. We can distinguish several possible cases using the discriminant,
The following cases need to be considered: [14]
- If Δ > 0, then the equation has three distinct real roots.
- If Δ = 0, then the equation has a multiple root and all its roots are real.
- If Δ < 0, then the equation has one real root and two nonreal complex conjugate roots.
[edit] General formula of roots
For the general cubic equation (1) with real coefficients, the general formula for the roots, in terms of the coefficients, is as follows if (2b3 − 9abc + 27a2d)2 − 4(b2 − 3ac)3 = − 27a2Δ > 0, i.e. if there are two non real roots:
However, this formula is wrong if the operand of the square root is negative or if the coefficients belong to a field which is not contained in the field of the real numbers: When this operand is real and positive, the cubic roots are real and well defined. In the other case, the square root is not real and one has to choose, once for all a determination for it, for example the one with positive imaginary part. For extracting the cubic roots we have also to choose a determination for the cubic roots, and this gives nine possible values for the first root of an equation which has only three roots.
A correct solution may be obtained by remarking that the proof of above formula shows that the product of the two cubic roots is rational. This gives the following formula in which 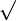 or
or ![sqrt[3]{ }](http://upload.wikimedia.org/math/9/b/b/9bbd095bafd3ae229d6baa25f34ebe84.png) stand for any determination of the square or cubic root, if
stand for any determination of the square or cubic root, if 
If  and b2 − 3ac = 0, the sign of Q has to be chosen for having
and b2 − 3ac = 0, the sign of Q has to be chosen for having  .
.
If Q = 0 and b2 − 3ac = 0, the three roots are equal:
If Q = 0 and  , above expression for the roots is correct but misleading, hiding the fact that no radical is needed to represent the roots. In fact, in this case, there is a double root
, above expression for the roots is correct but misleading, hiding the fact that no radical is needed to represent the roots. In fact, in this case, there is a double root

- and a simple root
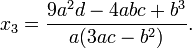
The next sections describe how these formulas may be obtained.
[edit] Reduction to a monic trinomial
Dividing Equation (1) by a and substituting x by  (Tschirnhaus transformation) we get the equation
(Tschirnhaus transformation) we get the equation
where
Any formula for the roots of Equation (2) may be transformed in a formula for the roots of Equation (1) by substituting p and q by the above values and using the relation  .
.
Therefore, only Equation (2) is considered in the following.
[edit] Cardano's method
The solutions can be found with the following method due to Scipione del Ferro and Tartaglia, published by Gerolamo Cardano in 1545.[15]
We first apply preceding reduction, giving the so-called depressed cubic
We introduce two variables u and v linked by the condition
and substitute this in the depressed cubic (2), giving
 .
.
At this point Cardano imposed a second condition for the variables u and v
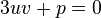 .
.
As the first parenthesis vanishes in (3), we get u3 + v3 = − q and u3v3 = − p3 / 27. Thus u3 and v3 are the two roots of the equation
At this point, Cardano, who did not know complex numbers, supposed that the roots of this equation were real, that is that 
Solving this equation and using the fact that u and v may be exchanged, we find
 and
and 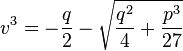 .
.
As these expressions are real, their cubic roots are well defined and, like Cardano, we get
The two complex roots are obtained by considering the complex cubic roots; the fact uv is real implies that they are obtained by multiplying one of the above cubic roots by  and the other by
and the other by  .
.
If  is not necessarily positive, we have to choose a cubic root of u3. As there is no direct way to choose the corresponding cubic root of v3, one has to use the relation
is not necessarily positive, we have to choose a cubic root of u3. As there is no direct way to choose the corresponding cubic root of v3, one has to use the relation 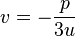 , which gives
, which gives
and
Note that the sign of the square root does not affect the resulting t, because changing it amounts to exchanging u and v. We have chosen the minus sign to have  when p = 0 and
when p = 0 and 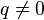 , in order to avoid a division by zero. With this choice, the above expression for t works always, except when p = q = 0, where the second term becomes 0/0. In this case there is a triple root t = 0.
, in order to avoid a division by zero. With this choice, the above expression for t works always, except when p = q = 0, where the second term becomes 0/0. In this case there is a triple root t = 0.
Note also that in several cases the solutions are expressed with less square or cubic roots
- If p = q = 0 then we have the triple real root
- If p = 0 and
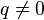 then
then ![u=-sqrt[3]{q} text{ and } v = 0](http://upload.wikimedia.org/math/2/1/c/21ce5e3b05a268ece1049819132e57ae.png) and the three roots are the three cubic roots of − q.
and the three roots are the three cubic roots of − q.
- If
 and q = 0 then
and q = 0 then - in which case the three roots are
- where
- Finally if
 , there is a double root and a simple root which may be expressed rationally in term of p and q, but this expression may not be immediately deduced from the general expression of the roots:
, there is a double root and a simple root which may be expressed rationally in term of p and q, but this expression may not be immediately deduced from the general expression of the roots:
To pass from these roots of t in Equation (2) to the general formulas for roots of x in Equation (1), subtract  and replace p and q by their expressions in terms of a,b,c,d.
and replace p and q by their expressions in terms of a,b,c,d.
[edit] Lagrange's method
In his paper Réflexions sur la résolution algébrique des équations (Thoughts on the algebraic solving of equations), Joseph Louis Lagrange introduced a new method to solve the equations of low degree.
This method works well for cubic and quartic equations, but Lagrange did not succeed in applying it to a quintic equation, because it implies to solve a resolving polynomial of degree at least six.[16][17][18] This is explained by the Abel–Ruffini theorem, which proves that such polynomials cannot be solved by radicals. Nevertheless the modern methods for solving solvable quintic equations are mainly based on Lagrange's method.[18]
In the case of cubic equations, Lagrange's method gives the same solution as Cardano's, but avoids its magic aspect (Why did Cardano choose these auxiliary variables?). Moreover it may also be applied directly to general cubic equation (1) without using the reduction to the trinomial equation (2). Nevertheless the computation is much easier on this reduced equation.
Suppose that x0, x1 and x2 are the roots of equation (1) or (2), and define  , so that ζ is a primitive third root of unity which satisfies the relation ζ2 + ζ + 1 = 0. We now set
, so that ζ is a primitive third root of unity which satisfies the relation ζ2 + ζ + 1 = 0. We now set
This is the discrete Fourier transform of the roots: observe that while the coefficients of the polynomial are symmetric in the roots, in this formula an order has been chosen on the roots, so these are not symmetric in the roots. The roots may then be recovered from the three si by inverting the above linear transformation via the inverse discrete Fourier transform, giving
The polynomial s0 is an elementary symmetric polynomial and is thus equal to − b / a in case of Equation (1) and to zero in case of Equation (2), so we only need to seek values for the other two.
The polynomials s1 and s2 are not symmetric functions or the roots: s0 is invariant, while the two non-trivial cyclic permutations of the roots send s1 to ζs1 and s2 to ζ2s2, or s1 to ζ2s1 and s2 to ζs2 (depending on which permutation), while transposing x1 and x2 switches s1 and s2; other transpositions switch these roots and multiply them by a power of ζ.
Thus,  ,
,  and s1s2 are left invariant by the cyclic permutations of the roots, which multiply them by ζ3 = 1. Also s1s2 and
and s1s2 are left invariant by the cyclic permutations of the roots, which multiply them by ζ3 = 1. Also s1s2 and  are left invariant by the transposition of x1 and x2 which exchanges s1 and s2. As the permutation group S3 of the roots is generated by these permutations, it follows that
are left invariant by the transposition of x1 and x2 which exchanges s1 and s2. As the permutation group S3 of the roots is generated by these permutations, it follows that  and s1s2 are symmetric functions of the roots and may thus be written as polynomials in the elementary symmetric polynomials and thus as rational functions of the coefficients of the equation. Let
and s1s2 are symmetric functions of the roots and may thus be written as polynomials in the elementary symmetric polynomials and thus as rational functions of the coefficients of the equation. Let  and s1s2 = B these expressions, which will be explicitly computed below.
and s1s2 = B these expressions, which will be explicitly computed below.
We have got that  and
and  are the two roots of the quadratic equation
are the two roots of the quadratic equation
Thus the resolution of the equation may be finished exactly as described for Cardano's method, with s1 and s2 in place of u and v.
[edit] Computation of A and B
Setting E1 = x0 + x1 + x2, E2 = x0x1 + x1x2 + x2x1 and E3 = x0x1x2, the elementary symmetric polynomials, we have, using that ζ3 = 1:
The expression for  is the same with ζ and ζ2 exchanged. Thus, using ζ2 + ζ = − 1 we get
is the same with ζ and ζ2 exchanged. Thus, using ζ2 + ζ = − 1 we get
and a straightforward computation gives
Similarly we have
When solving Equation (1) we have
- E1 = − b / a, E2 = c / a and E3 = − d / a
With Equation (2), we have E1 = 0, E2 = p and E3 = − q and thus:
- A = − 27q and B = − 3p.
Note that with Equation (2), we have  and s1s2 = − 3p, when in Cardano's method we have set x0 = u + v and
and s1s2 = − 3p, when in Cardano's method we have set x0 = u + v and  Thus we have, up to the exchange of u and v:
Thus we have, up to the exchange of u and v:
- s1 = 3u and s2 = 3v.
In other words, in this case, Cardano's and Lagrange's method compute exactly the same things, up to a factor of three in the auxiliary variables, the main difference being that Lagrange's method explains why these auxiliary variables appear in the problem.
[edit] Trigonometric (and hyperbolic) method
When a cubic equation has three real roots, the formulas expressing these roots in term of radicals involve complex numbers. A representation of these roots in term of cosine and arccosine allows to avoid complex numbers. The formulas which follow are true in general (except when p=0), but involve complex cosine and arccosine when there is only one real root.
Starting from Equation (2), t3 + pt + q = 0, let us set  The idea is to choose u for identifying Equation (2) with the identity
The idea is to choose u for identifying Equation (2) with the identity
In fact, choosing  and dividing Equation (2) by
and dividing Equation (2) by  we get
we get
Combining with above identity, we get
and thus the roots are[19]
This formula is totally real if p < 0 and the argument of the arccosine is between -1 and 1. The last condition is equivalent with  which implies also p < 0. Thus the above formula for the roots is totally real if and only if the three roots are real.
which implies also p < 0. Thus the above formula for the roots is totally real if and only if the three roots are real.
Denoting by C(p,q) the above value of t0 and using the inequality  for a real number u such that
for a real number u such that  the three roots may also be expressed as
the three roots may also be expressed as
If the three roots are real, we have
All these formulas may be straightforwardly transformed into formulas for the roots of the general cubic equation (1), using the back substitution described in Section Reduction to a monic trinomial.
When there is only one real root (and p≠0), it may be similarly represented, using hyperbolic functions, as[20]
If p≠0 and the inequalities on the right are not satisfied the formulas remain valid but involve complex quantities.
When  , above values of t0 are sometimes named Chebyshev cube root.[21] More precisely the values involving cosines and hyperbolic cosines define, when p = − 3, the same analytic function denoted
, above values of t0 are sometimes named Chebyshev cube root.[21] More precisely the values involving cosines and hyperbolic cosines define, when p = − 3, the same analytic function denoted  , which is the proper Chebyshev cube root. The value involving hyperbolic sines is similarly denoted
, which is the proper Chebyshev cube root. The value involving hyperbolic sines is similarly denoted  when p = 3.
when p = 3.
[edit] Factorization
If r is any root of (1), then we may factor using r to obtain
Hence if we know one root we can find the other two by solving a quadratic equation, giving
for the other two roots.
Hope it workz....for u!
Cheerz...Thumb up Plz....!
- 0




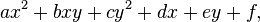


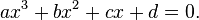
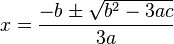

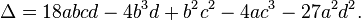
![begin{align}
x_1 =
&-frac{b}{3 a}
&-frac{1}{3 a} sqrt[3]{tfrac12left[2 b^3-9 a b c+27 a^2
d+sqrt{left(2 b^3-9 a b c+27 a^2 dright)^2-4 left(b^2-3 a
cright)^3}right]}
&-frac{1}{3 a} sqrt[3]{tfrac12left[2 b^3-9 a b c+27 a^2
d-sqrt{left(2 b^3-9 a b c+27 a^2 dright)^2-4 left(b^2-3 a
cright)^3}right]}
x_2 =
&-frac{b}{3 a}
&+frac{1+i sqrt{3}}{6 a} sqrt[3]{tfrac12left[2 b^3-9 a b c+27
a^2 d+sqrt{left(2 b^3-9 a b c+27 a^2 dright)^2-4 left(b^2-3 a
cright)^3}right]}
&+frac{1-i sqrt{3}}{6 a} sqrt[3]{tfrac12left[2 b^3-9 a b c+27
a^2 d-sqrt{left(2 b^3-9 a b c+27 a^2 dright)^2-4 left(b^2-3 a
cright)^3}right]}
x_3 =
&-frac{b}{3 a}
&+frac{1-i sqrt{3}}{6 a} sqrt[3]{tfrac12left[2 b^3-9 a b c+27
a^2 d+sqrt{left(2 b^3-9 a b c+27 a^2 dright)^2-4 left(b^2-3 a
cright)^3}right]}
&+frac{1+i sqrt{3}}{6 a} sqrt[3]{tfrac12left[2 b^3-9 a b c+27
a^2 d-sqrt{left(2 b^3-9 a b c+27 a^2 dright)^2-4 left(b^2-3 a
cright)^3}right]}
end{align}](http://upload.wikimedia.org/math/7/f/1/7f19af779a9bea4db300039405693001.png)
![begin{align}
Q = &sqrt{(2 b^3-9 a b c+27 a^2 d)^2-4 (b^2-3 a c)^3}
C = &sqrt[3]{tfrac12 (Q + 2 b^3-9 a b c+27 a^2 d)}
x_1 = &-frac{b}{3 a}-frac{C}{3 a}-frac{b^2-3 a c}{3 a C}
x_2 = &-frac{b}{3 a}+frac{C(1+i sqrt{3})}{6 a} +frac{(1-i
sqrt{3}) (b^2-3 a c)}{6 a C}
x_3 = &-frac{b}{3 a}+frac{C(1-i sqrt{3})}{6 a} +frac{(1+i
sqrt{3}) (b^2-3 a c)}{6 a C}
end{align}](http://upload.wikimedia.org/math/3/4/8/348ffa4b63eb0ddd0c4391c9605e6865.png)

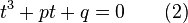




![t_1=u+v=sqrt[3]{-{qover 2}+
sqrt{{q^{2}over 4}+{p^{3}over 27}}} +sqrt[3]{-{qover 2}-
sqrt{{q^{2}over 4}+{p^{3}over 27}}}](http://upload.wikimedia.org/math/6/2/1/621f6bb67577ad721951719e7b662f0a.png)
![u=sqrt[3]{-{qover 2}- sqrt{{q^{2}over
4}+{p^{3}over 27}}} qquad (4)](http://upload.wikimedia.org/math/e/7/7/e77e15ea1779eb73fc57728535517c0b.png)