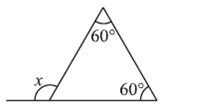
The exterior angle theorem is a theorem in elementary geometry which states that the exterior angle of a triangle is equal to the sum of the two remote interior angles.
A triangle has three corners, called vertices. The sides of a triangle that come together at a vertex form an angle. This angle is called the interior angle. In the picture below, the angles a, b and c are the three interior angles of the triangle. An exterior angle is formed by extending one of the sides of the triangle; the angle between the extended side and the other side is the exterior angle. In the picture, angle d is an exterior angle.
The exterior angle theorem says that the size of an exterior angle at a vertex of a triangle equals the sum of the sizes of the interior angles at the other two vertices of the triangle. So, in the picture, the size of angle d equals the size of angle a plus the size of angle c.
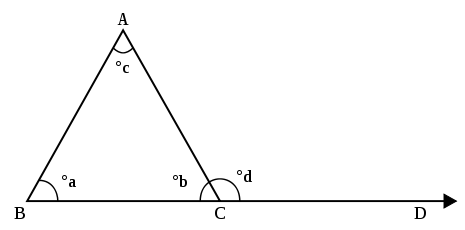
Given: In ∆ABC, angle ACD is the exterior angle.
To prove: 
ACD = ABC + BAC (here, ACD denotes the size of the angle ACD)
Proof:
| Statements | Reason |
|---|
| In ∆ABC, a + b + c = 180°------[1] | Sum of the measures of all the angles of a triangle is 180° |
| Also, b + d = 180°-------[2] | Linear pair axiom |
| ∴ a + c + b = b + d | From [1] and [2] |
∴ a + c + b = b +md | |
| ∴ d = a + c |
| i.e. ACD = ABC + BAC | |
Hence, proved.
Best Wishes !@
