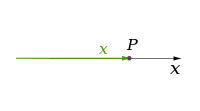
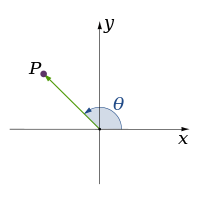
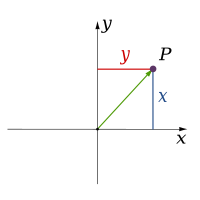
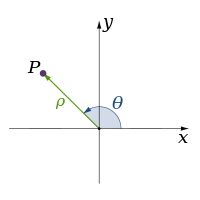
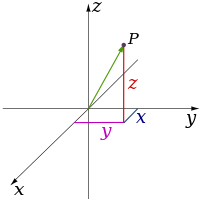
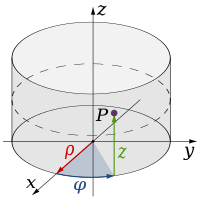
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number ofcoordinates needed to specify any point within it.[1][2] Thus a line has a dimension of one because only one coordinate is needed to specify a point on it (for example, the point at 5 on a number line). A surface such as a plane or the surface of acylinder or sphere has a dimension of two because two coordinates are needed to specify a point on it (for example, to locate a point on the surface of a sphere you need both its latitude and its longitude). The inside of a cube, a cylinder or a sphere is three-dimensional because three co-ordinates are needed to locate a point within these spaces.
In physical terms, dimension refers to the constituent structure of all space (cf. volume) and its position in time (perceived as a scalar dimension along the t-axis), as well as the spatial constitution of objects within—structures that correlate with both particle and field conceptions, interact according to relative properties of mass—and are fundamentally mathematical in description. These, or other axes, may be referenced to uniquely identify a point or structure in its attitude and relationship to other objects and occurrences. Physical theories that incorporate time, such as general relativity, are said to work in 4-dimensional "spacetime", (defined as a Minkowski space). Modern theories tend to be "higher-dimensional" including quantum field and string theories. The state-space of quantum mechanics is an infinite-dimensional function space.
The concept of dimension is not restricted to physical objects. High-dimensional spaces occur in mathematics and the sciences for many reasons, frequently as configuration spaces such as in Lagrangian or Hamiltonian mechanics; these are abstract spaces, independent of the physical space we live in.
| Number of dimensions | Example co-ordinate systems |
|---|
| 1 | |
| 2 | |
| 3 | |