Chapter 1: Sets
❖ A set is a well-defined collection of objects.
• Example: The collection of all rational numbers less than 10 is a set whereas the collection of all the brilliant students in a class is not a set.
• Sets are usually denoted by capital letters A, B, S, etc.
• The elements of a set are usually denoted by small letters a, b, t, u, etc.
❖ If x is an element of a set S, then we say that “x belongs to S”. Mathematically, we write it as x ∈ S. If y is not an element of a set S, then we say that “y does not belong to S”.
Mathematically, we write it as y ∈ S.
❖ Methods for representing a set
• Roster or tabular form: In this form, all the elements of a set are listed, separated by commas and enclosed within braces { }.
In this form, the order in which the elements are listed is immaterial, and the elements are not repeated.
Example: The set of letters forming the word ‘TEST’ is {T, E, S}.
• Set-builder form: In this form all the elements of a set possess a single common property which is not possessed by any element outside the set.
Example: The set {2, –2} can be written in the set-builder form as {x : x is an integer and x2 – 4 = 0}.
❖ Types of sets
• A set which does not contain any element is called an empty set or a null set or a void set. It is denoted by the symbol ϕ or { }.
Example: The set {x : x ∈ N, x is an even number and 8 < x < 10} is an empty set.
• A set which is empty or consists of a definite number of elements is called finite; otherwise, the set is called infinite.
Example: The set {x : x ∈ N and x is a square number} is an infinite set. The set {x : x ∈
N and x2 – 2x – 3 = 0} is a finite set as it is equal to {–1, 3}.
❖ All infinite sets cannot be described in the roster form.
For example, the set of rational numbers cannot be described in this form. This is because the elements of this set do not follow any particular pattern.
❖ Two sets A and B are said to be equal if they have exactly the same elements and we write A = B; otherwise, the sets are said to be unequal and we write A ≠ B.
Example: The sets A = {x :x ∈ N and (x – 1)(x + 4) = 0} and B = {–4, 1} are equal sets.
❖ A set does not change if one or more elements of the set are repeated.
Example: The sets A = {E, L, E, M, E, N, T, S} and B = {E, L, M, N, T, S} are equal since each element of A is in B, and vice-versa.
❖ Subsets
• A set A is said to be a subset of a set B if every element of A is also an element of B and we write A ⊂ B.
In other words, A ⊂ B if a ∈ A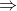 a ∈ B.
a ∈ B.
• A ⊂ B and B ⊂ A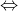 A = B
A = B
• An empty set is a subset of every set.
• Every set is a subset of itself.
• If A ⊂ B and A ≠ B, then A is called a proper subset of B, and B is called a superset of A.
❖ If a set has only one element, then it is called a singleton set.
Example: A = {–17} is a singleton set.
❖ Intervals as subsets of R
Let a, b ∈ R and a < b. Then,
• {y : a < y < b} is called an open interval and is denoted by (a, b).
In the open interval (a, b), all the points between a and b belong to the open interval (a, b), but a, b themselves do not belong to this interval.
• {y : a ≤ y ≤ b}is called a closed interval and is denoted by [a, b]. In this interval, all the points between a and b as well as the points a and b are included.
• [a, b) = {y : a ≤ y < b}is an open interval from a to b, including a, but excluding b.
• (a, b] = {y : a < y ≤ b}is an open interval from a to b, including b, but excluding a.
❖ Power set
• The collection of all subsets of a set A is called the power set of A. It is denoted by P(A).
• If A is a set with n(A) = m, then n[P(A)] = 2m.
❖ Venn diagrams
Most of the relationships between sets can be represented by means of diagrams known as Venn diagrams.
❖ A universal set is the super set of all sets under consideration and is denoted by U.
❖ Union of sets
• The union of two sets A and B is the set which contains all those elements which are only in A, only in B and in both A and B, and this set is denoted by ‘A ⋃ B’.
A ⋃ B = {x: x ∈ A or x ∈ B}
• Properties of union of sets
(i) A⋃B = B⋃A (Commutative Law)
(ii) (A⋃B) ⋃C = A⋃(B⋃C) (Associative Law)
(iii) A⋃ϕ = A (ϕ is the identity of ⋃)
(iv) A⋃A = A (Idempotent Law)
(v) U⋃A = U (Law of U)
❖ Intersection of sets
• The intersection of two sets A and B is the set of all those elements which belong to both A and B. It is denoted by ‘A ⋂ B’.
• Properties of intersection of sets
(i) A ⋂ B = B ⋂ A (Commutative Law)
(ii) (A ⋂ B) ⋂ C = A ⋂(B ⋂ C) (Associative Law)
(iii) ϕ ⋂ A = ϕ (Law of ϕ)
(iv) U ⋂ A = A (Law of U)
(v) A ⋂ A = A (Idempotent Law)
(vi) A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C) (Distributive law of ⋂ on ⋃)
(vii) A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)
❖ Difference of sets
• The difference between the sets A and B (i.e., A – B, in this order) is the set of the elements which belong to A, but not to B.
A – B = {x: x ∈ A and x ∉ B}
• Properties of operation of difference of sets
(i) A – B =A – (A ⋂ B)
(ii) For A ≠ B, A – B ≠ B – A
(iii) For A = B, A – B = B – A = ϕ
(iv) For B = ϕ, A – B = A and B – A = ϕ
(v) A – U = ϕ
(vi) For A ⊂ B, A – B = ϕ; for this reason, A – U = ϕ
❖ The sets A – B, A ⋂ B and B – A are mutually disjoint sets, i.e., the intersection of any of these two sets is a null set.
.png)
❖ Complement of a set
• If U is a universal set and A is a subset of U, then the complements of A are denoted by the set A'. This is the set of all element of U which are not the elements of A.
A' = {x: x ∈U and x∉ A} = U – A
A' is also the subset of U
• Properties of complement of a set
(i) (A')' =A
(ii) A ⋃ A' = U
(iii) A ⋂ A' = ϕ
(iv) ϕ' = U and U' = ϕ
• De Morgan’s laws
For any sets A and B,
(i) (A ⋃ B)' = A' ⋂ B'
(ii) (A ⋂ B)' = A' ⋃ B'
❖ If A and B are finite sets, such that A ⋂ B = ϕ, then n(A ⋃ B) = n(A) + n(B)
❖ If A and B are finite sets, such that A ⋂ B ≠ ϕ, then, n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B)
If A, B and C are finite sets, then n(A ⋃ B ⋃ C) = n(A) + n(B) + n(C) – n (A ⋂ B) – n(B ⋂ C) – n(A ⋂ C) + n(A ⋂ B ⋂ C)Chapter 2: Relations and Functions
❖ Cartesian product of sets
• Two non-empty sets P and Q are given. The Cartesian product P × Q is the set of all ordered pairs of elements from P and Q, i.e.,
P × Q = {(p,q): p ∈ P and q ∈Q}
• If either P or Q is a null set, then P × Q will also be a null set, i.e., P × Q = ϕ.
In general, if A is any set, then A × ϕ = ϕ.
• Two ordered pairs are equal if and only if the corresponding first elements are equal and the second elements are also equal. In other words, if (a, b) = (x, y), then a = x and b = y.
❖ For any two sets A and B
• A × B ≠ B × A
• If n(A) = p, n(B) = q, then n(A × B) = pq
• If A and B are non-empty sets and either A or B is an infinite set, then so is the case with A × B
❖ A × A × A = {(a, b, c) : a, b, c ∈ A}. Here, (a, b, c) is called an ordered triplet.
❖ Relation
A relation R from a set A to a set B is a subset of the Cartesian product A × B, obtained by describing a relationship between the first element x and the second element y of the ordered pairs (x, y) in A × B.
• The image of an element x under a relation R is y, where x, y ∈ R.
• The set of all the first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R.
• The set of all the second elements in a relation R from a set A to a set B is called the range of the relation R. The whole set B is called the co-domain of the relation R.
Range ⊆ Co-domain
❖ The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A × B.
If n(A) = p and n(B) = q, then n(A × B) = pq and the total number of relations is 2pq.
❖ Functions
A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.
In other words, a function f is a relation from a non-empty set A to another non-empty set B, such that the domain of f is A and no two distinct ordered pairs in f have the same first element.
• The function f from A to B is denoted by f : A → B. Here, A is the domain and B is the co-domain of f.
• If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f, and a is called the pre-image of b under f.
• A function having either R (real numbers) or one of its subsets as its range is called a real-valued function. Further, if its domain is also either R or a subset of R, it is called a real function.
❖ Types of functions
• Identity function: The function f: R → R defined by y = f(x) = c, for each x ∈ R, is called the identity function.
Here, R is the domain and range of f.
• Constant function: The function f: R → R defined by y = f(x) = c, for each x ∈ R, where c is a constant, is a constant function.
Here, the domain of f is R and its range is {c}.
• Polynomial function: A function f: R → R is said to be a polynomial function if for each x ∈ R, , where n is a non-negative integer and .
• Rational function: The functions of the type , where f(x) and g(x) are polynomial functions of x defined in a domain and where g(x) ≠ 0, are called rational functions.
• Modulus function: The function f: R → R defined by f(x) = |x|, for each x ∈ R, is called the modulus function.
In other words,
• Signum function: The function f: R → R defined by
is called the signum function. Its domain is R and its range is the set {–1, 0, 1}.
• Greatest Integer function: The function f: R → R defined by f(x) = [x], x ∈ R, assuming the value of the greatest integer less than or equal to x, is called the greatest integer function.
• Linear function: The function f defined by f(x) = mx + c, for x ∈ R, where m and c are constants, is called the linear function. Here, R is the domain and range of f.
❖ Algebra of functions
For functions f: X → R and g: X → R, we define
• (f + g): X → R by (f + g) (x) = f(x) + g (x), x ∈ X
• (f – g): X → R by (f – g) (x) = f(x) – g (x) x ∈ X
• (fg): X → R by (fg) (x) = f(x) . g(x), x ∈ X
• (af): X → R by (α f)(x) = α f(x), x ∈ X and α is a real number
• , x ∈ X and g(x) ≠ 0.Chapter 3: Trigonometric Functions
❖ Consider a circle of radius r having an arc of length l that subtends an angle of θ radians.
Then, l = rθ.
❖ Relation between radian and degree measure
Radian measure =
❖ A degree is divided into 60 minutes and a minute is divided into 60 seconds. One sixtieth of a degree is called a minute, written as 1', and one sixtieth of a minute is called a second, written as 11".
Thus, 10 = 60' and 1' = 60"
❖ Domain and range of trigonometric functions
❖ Signs of trigonometric functions in different quadrants
❖ Trigonometric identities
•
•
•
•
• cos2 x + sin2 x = 1
• 1 + tan2 x = sec2 x
• 1 + cot2 x = cosec2x
❖ Trigonometric ratios of allied angles
• sin (–x) = – sin x
• cos (–x) = cos x
•
•
•
•
• cos (π – x) = – cos x
• sin (π – x) = sin x
• cos (π + x) = – cos x
• sin (π + x) = – sin x
• cos (2π – x) = cos x
• sin (2π – x) = – sin x
• cos (2nπ + x) = cos x, n ∈ Z
• sin (2nπ + x) = sin x, n ∈ Z
❖ Sum and difference of two angles
• sin (x + y) = sin x cos y + cos x sin y
• cos (x + y) = cos x cos y – sin x sin y
• sin (x – y) = sin x cos y – cos x sin y
• cos (x – y) = cos x cos y + sin x sin y
• If none of the angles x, y and (x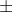 y)is an odd multiple of , then
y)is an odd multiple of , then
• If none of the angles x, y and (x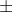 y) is a multiple of π, then
y) is a multiple of π, then
❖ Trigonometric ratios of multiple angles
•
•
•
• sin 3x = 3 sin x – 4 sin3 x
• cos 3x = 4 cos3x – 3 cos x
•
❖ Some more trigonometric identities
•
•
•
•
• 2 cos x cosy = cos (x + y) + cos (x – y)
• –2 sin x sin y = cos (x + y) – cos (x – y)
• 2 sin x cos y = sin (x + y) + sin (x – y)
• 2 cos x sin y = sin (x + y) – sin (x – y)
❖ General solutions of trigonometric equations
•
•
•
•
• Chapter 4: Principle of Mathematical Induction
❖ There are some mathematical statements or results that are formulated in terms of n, where n is a positive integer. To prove such statements, the well-suited principle that is used, based on the specific technique, is known as the principle of mathematical induction.
❖To prove a given statement in terms of n, we assume the statement to be P(n).
1. Thereafter, we examine the correctness of the statement for n = 1 i.e., for P(1) to be true.
2. Then, assuming that the statement is true for n = k, where k is a positive integer, we prove that the statement is true for n = k + 1 i.e., the truth of P(k) implies the truth of P
(k + 1). Then, we say that P(n) is true for all natural numbers n.
Example: For all n∈N, prove that
Solution:
Let the given statement be P(n), i.e.,
For n = 1, , which is true.
Now, assume that P(x) is true for some positive integer k. This means
We shall now prove that P(k + 1) is also true.
Now, we have
Thus, P(k + 1) is true whenever P(k) is true. Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.Chapter 5: Complex Numbers and Quadratic Equations
❖ A number of the form a + ib, where a and b are real numbers and , is defined as a complex number.
• For the complex numbers z = a + ib, a is called the real part (denoted by Re z) and b is called the imaginary part (denoted by Im z) of the complex number z.
❖ Two complex numbers z1 = a + ib and z2 = c + id are equal if a = c and b = d.
❖ Addition of complex numbers
• Let z1 = a + ib and z2 = c + id be any two complex numbers. The sum is defined as z1 + z2 = (a + c) + i (b + d).
• Properties of addition of complex numbers
(i) Closure law: Sum of two complex numbers is also a complex number.
(ii) Commutative law: For two complex numbers z1 and z2, z1 + z2 = z2 + z1
(iii) Associative law: For any three complex numbers z1, z2 and z3, (z1 + z2) + z3 = z1 + (z2 + z3)
(iv) Existence of additive identity: There exists a complex number 0 + i0 (denoted by 0), called the additive identity or zero complex number, such that for every complex number z, z + 0 = z
(v) Existence of additive inverse: For every complex number z = a+ ib, there exists a complex number –a + i(–b) [denoted by –z], called the additive inverse or negative of z, such that z + (–z) = 0
❖ Given any two complex numbers z1, and z2, the difference z1 - z2 is defined as z1 - z2 = z1 + (– z2)
❖ Multiplication of complex numbers
• For two complex numbers z1 and z2, such that z1 = a + ib and z2 = c + id, the multiplication is defined as z1 z2 = (ac - bd) + i(ad + bc).
• Properties of multiplication of complex numbers
(i) Closure law: The product of two complex numbers is also a complex number.
(ii) Commutative law: For any two complex numbers z1 and z2, z1z2 = z2z1.
(iii) Associative law: For any three complex numbers z1, z2 and z3, (z1z2) z3 = z1 (z2z3)
(iv) Existence of multiplicative identity: There exist a complex number 1 + i 0 (denoted as 1), called the multiplicative identity, such that for every complex numbers z, z.1 = z
(v) Existence of multiplicative inverse: For every non-zero complex number z = a + ib a ≠ 0, b ≠ 0, we have the complex number
(denoted by or z–1), called the multiplicative inverse of z, such that=1
(vi) Distributive law: For any three complex numbers z1, z2 and z3, z1 (z2 + z3) = z1z2 + z1z3
(z1 + z2) z3 = z1z3 + z2z3
❖ Given any two complex number z1 and z2, where z2 ≠ 0, the quotient is defined as
❖ Powers of i
For any integer
❖ If a and b are negative real numbers, then .
❖ Identities for complex numbers
For two complex numbers z1 and z2
•
•
•
•
•
❖ Modulus and conjugate of complex numbers
• The modulus of a complex number z = a + ib, is denoted by |z|, and is defined as the non-negative real number, i.e., .
• The conjugate of a complex number z = a + ib, is denoted by , and is defined as the complex number a – ib, i.e., .
❖ Properties of modulus and conjugate of complex numbers
For any three complex numbers z, z1, z2,
•
•
•
•
•
•
❖ The polar form of the complex number z = x + iy, is r(cos + sin
+ sin ), where (modulus of z) and .
), where (modulus of z) and .
The value of is such that –π <
is such that –π < 
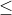 π, which is called the principle argument of z.
π, which is called the principle argument of z.
Example: Represent the complex number in polar form.
Solution:
Let
By squaring and adding them, we have
Thus,
Thus, the required polar form is 2.
❖ A polynomial equation of n degree has n roots.
❖ The solutions of the quadratic equation ax2 + bx + c = 0, where a, b, c ∈ R, a ≠ 0 and b2 – 4ac < 0, are given by .Chapter 6: Linear Inequalities
❖ Two real numbers or two algebraic expressions related by the symbol ‘<’, ‘>’, ‘≤’ or ‘≥’ form an inequality.
❖ The solution of an inequality in one variable is a value of the variable which makes it a true statement.
❖ Solution of linear inequalities in one variable
• Solving an inequality algebraically
(i) Equal numbers may be added to or subtracted from both sides of an inequality without affecting the sign of the inequality.
(ii) Both sides of an inequality can be multiplied with or divided by the same positive number. But when both sides are multiplied with or divided by a negative number, the sign of inequality is reversed.
• Graphical representation of Solution
(i) To represent x < a (or x > a) on a number line, encircle the number a, and darken the line to the left (or the right) of a.
(ii) To represent x ≤ a (or x ≥ a) on a number line, encircle the number a, and darken the line to the left (or the right) of a.
Example:
Solve 5(x – 3) ≤ 2x + 9
Solution:
5(x – 3) ≤ 2x + 9
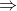 5x – 15 ≤ 2x + 9
5x – 15 ≤ 2x + 9
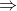 5x – 15 – 2x ≤ 2x + 9 – 2x
5x – 15 – 2x ≤ 2x + 9 – 2x
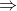 3x – 15 ≤ 9
3x – 15 ≤ 9
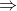 3x ≤ 9 + 15
3x ≤ 9 + 15
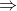 3x ≤ 24
3x ≤ 24
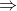 x ≤ 8
x ≤ 8
Thus, the solution of the given inequality can be represented on the number line as shown below:

❖ Graphical solution of linear inequalities in two variables
• The solution region of a system of inequalities is the region which satisfies all the given inequalities in the system simultaneously.
• In order to identify the half plane represented by an inequality, it is sufficient to take any point (a, b) (not on the line) and check whether it satisfies the inequality or not.
If it satisfies, then the inequality represents the half plane containing the point and we shade this region.
If not, then the inequality represents the half plane which does not contain the point. For convenience, the point (0, 0) is preferred.
• In an inequality of the type ax + by ≥ c or ax + by ≤ c, the points on the line ax + by = c are to be included in the solution region. So, we darken the line in the solution region.
• In an inequality of the type ax + by > c or ax + by < c, the points on the line ax + by = c are not to be included in the solution region. So, we draw a broken or dotted line in the solution region.
Example:
Solve the following system of linear inequalities graphically: 2x – y ≤ 4, x < 2
Solution:
The given linear inequalities are
2x – y ≤ 4 ...(i)
x < 2 ...(ii)
The graphs of the lines 2x – y = 4 and x = 2 are drawn in the figure below.
.png)
Inequality (i) represents the region on the left of the line 2x – y = 4 (including the line 2x – y = 4). Inequality (ii) represents the region on the left of the line x = 2 (excluding the line x = 2).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region, including the points on the line 2x – y = 4.Chapter 7: Permutations and Combinations
❖ If an event occurs in m different ways, following which another event occurs in n different ways, then the total number of occurrence of the events in the given order is m × n.
This is called the fundamental principle of counting.
❖ A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.
❖ Factorial notation
• The notation n! represents the product of the first n natural numbers, i.e., n! = 1 × 2 × 3 × ………× n
• 0! = 1
❖ The number of permutations of n different things taken r at a time,
• When repetition is not allowed, is denoted by nPr and is given by .
• When repetition is allowed, is nr.
❖ Permutations when all the objects are not distinct
• The number of permutations of n objects, when p objects are of the same kind and the rest are all different, is .
• The number of permutations of no objects, where p1 objects are of one kind, p2 are of the second kind , …………. , pk are of the kth kind and the rest, if any, are of different kinds, is .
❖ A combination is different selections of a number of objects taken a few or all at a time, irrespective of their arrangements.
❖ The number of combinations of n different things taken r at a time is denoted by nCr, which is given by
❖ Properties of nCr
•
•
• Chapter 8: Binomial Theorem
❖ The coefficients of the expansions of a binomial are arranged in an array. This array is called Pascal’s triangle. It can be written as:
❖ Binomial theorem for any positive integer
• The expansion of a binomial for any positive integral n is as follows:
• Some points about Binomial Theorem
(i) The notation stands for
Hence, the binomial theorem can also be stated as follows:
(ii) The coefficients of nCk occurring in the binomial theorem are known as binomial coefficients
(iii) In the expansion of (a + b)n, there are (n + 1) terms i.e., one more than the index.
(iv) In the successive terms of the expansion of (a + b)n, the index of a goes on decreasing by unity, starting with n in the first term and ending with 0 in the last term. Also, the index of b increases by unity, starting with 0 in the first term and ending with n in the last term.
(v) In every term of the expansion, the sum of the indices of a and b is n.
❖ In the binomial expansion of (a + b)n, taking a = x and b = – y, we have
❖ The (r + 1)th term (denoted by Tr + 1) is known as the general term of the expansion (a + b)n and it is given by
❖ Middle term in the expansion of (a + b)n
• If n is even, then the number of terms in the expansion will be n + 1. Since n is even, n + 1 is odd. Therefore, the middle term is term.
• If n is odd, then n + 1 is even. So, there will be two middle terms in the expansion. They are term and term.Chapter 9: Sequences and Series
❖ A sequence is an arrangement of numbers in definite order according to some rule.
• A sequence may be defined as a function whose domain is the set of natural numbers or some subset of the type {1, 2, 3… k}.
• A sequence containing finite number of terms is called a finite sequence, whereas a sequence containing infinite number of terms is called an infinite sequence.
❖ The general form of a sequence is a1, a2, a3, … an –1 , an, …
• a1, a2 … etc. are called the terms of the sequence.
• The nth term of the sequence, an, is called the general term of the sequence.
❖ An arrangement of numbers such as 1, 2, 4, 6, 10 … has no visible pattern. However, the sequence is generated by the recurrence relation given by
This sequence is called the Fibonacci sequence.
❖ Let a1, a2,… an –1,… be a given sequence. Accordingly, the sum of this sequence is given by the expression a1+ a2+…+an +...
This is called the series associated with the given sequence.
• The series is finite or infinite according as the given sequence.
• A series is usually represented in a compact form using sigma notation (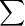 ).
).
This means the series a1+ a2+...+ an –1+ an can be written as
❖ Arithmetic progression
The sequence a1, a2,… an … is called an arithmetic sequence or an arithmetic progression (A.P.) if. an +1 = an + d, n ∈N.
Here, a1is called the first term and d is called the common difference of the A.P.
In standard form, the A.P. is written as a, a + d, a + 2d…
• The nth or the general term of an A.P. is given by an = a + (n – 1) d.
• If a is the first term, d is the common difference, l is the last term and n is the number of terms, then l = a + (n – 1) d.
• The sum of n terms of an A.P. (denoted by Sn) is given by
❖ Properties of an A.P.
• If a constant is added or subtracted or multiplied to each term of an A.P., then the resulting sequence is also an A.P.
• If each term of an A.P. is multiplied or divided by a non-zero constant, then the resulting sequence is also an A.P.
❖ Arithmetic mean
• For any two numbers a and b, we can insert a number A between them such that a, A, b is an A.P.
Here, A is called the arithmetic mean (A.M.) of numbers a and b and .
• Let A1, A2… An be n numbers between a and b such that a, A1, A2,…, An, b is an A.P.
Accordingly, common difference (d) is given by .
The numbers A1, A2… An are given as follows:
❖ Geometric progression
A sequence is said to be a geometric progression (G.P.) if the ratio of any term to its preceding term is the same throughout. This constant factor is called the common ratio and it is denoted by r.
In standard form, the G.P. is written as a, ar, ar2… where, a is the first term and r is the common ratio.
• The nth term (or general term) of a G.P. is given by an = ar n – 1
• The sum of n terms (Sn) of a G.P. is given by
❖ Geometric mean
• For any two positive numbers a and b, we can insert a number G between them such that a, G, b is a G.P. G is called a geometric mean (G.M.) and is given by
• Let G1, G2, …,Gn be n numbers between positive numbers a and b such that a, G1, G2, …, Gn, b is a G.P. Common ratio of G.P.,
Therefore, G1= ar, G2 = ar2,…, Gn = arn
❖ Let A and G be the respective A.M. and G.M. of two given positive real numbers a and b.
•
• A ≥ G
❖ Sum of n-terms of some special series
• Sum of first n natural numbers
• Sum of squares of the first n natural numbers
• Sum of cubes of the first n natural numbers
Chapter 10: Straight Lines
❖ Slope of a line
If is the inclination of a line l (the angle between positive x-axis and line l), then tan
is the inclination of a line l (the angle between positive x-axis and line l), then tan  is called the slope or gradient of line l.
is called the slope or gradient of line l.
.png)
The slope of a line is denoted by m.
Thus, m = tan ,
,  ≠ 90°
≠ 90°
• The slope of a line whose inclination is 90º is not defined. Hence, the slope of the vertical line (y-axis) is undefined.
• The slope of the horizontal line (x-axis) is zero.
❖ The slope (m) of a non-vertical line passing through the points (x1, y1) and (x2, y2) is given by .
❖ Suppose l1 and l2 are non-vertical lines having slopes m1 and m2 respectively
• l1 is parallel to l2 if and only if m1 = m2, i.e., their slopes are equal.
• l1 is perpendicular to l2 if and only if m1m2 = –1, i.e., the product of their slopes is –1.
• An acute angle, , between l1 and l2 is given by
, between l1 and l2 is given by
❖ Three points A, B and C are collinear if and only if
Slope of AB = Slope of BC
❖ Horizontal and vertical lines
• The equation of a horizontal line at distance a from the x-axis is either y = a (above x-axis) or y = – a (below y-axis).
• The equation of a vertical line at distance b from the y-axis is either x = b (right of y-axis) or x = – b (left of y-axis).
❖ Point-slope form of a line
The point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates satisfy the equation. This means y – y0 = m (x – x0).
❖ Two-point form of a line
The equation of the line passing through the points (x1, y1) and (x2, y2) is given by
.
❖ Slope-intercept form of a line
• The equation of the line, with slope m, which makes y-intercept c is given by y = mx + c.
• The equation of the line, with slope m, which makes x-intercept d is given by y = m(x – d).
❖ Intercept form of a line
The equation of the line making intercepts a and b on x-axis and y-axis respectively is
❖ Normal form of a line
The equation of the line at normal distance p from the origin and angle which the normal makes with the positive direction of the x-axis is given by x cos
which the normal makes with the positive direction of the x-axis is given by x cos  + y sin
+ y sin  = p
= p
❖ Any equation of the form Ax + By + C = 0, where A and B are not zero simultaneously is called the general linear equation or general equation of line.
❖ The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is
.
❖ The distance (d) between two parallel lines i.e., Ax + By + C1 = 0 and Ax + By + C2 = 0 is given by
Chapter 11: Conic Sections
❖ Conic sections or conics are the curves that are obtained by intersecting a plane with a double-napped right circular cone. Circles, ellipses, parabolas and hyperbolas are examples of conic sections.
❖ A double-napped cone can be obtained by rotating a line (let us say m) about a fixed vertical line (let us say l).
.png)
Here, the fixed line l is called the axis of the cone and m is called the generator of the cone. The intersection (V) of l and m is called the vertex of the cone.
❖ Different conics formed by intersecting a plane and a double-napped cone
If 1 is the angle between the axis and the generator and
1 is the angle between the axis and the generator and  2 is the angle between the plane and the axis, then, for different conditions of
2 is the angle between the plane and the axis, then, for different conditions of  1 and
1 and  2, we get different conics, which are described with the help of a table as shown below.
2, we get different conics, which are described with the help of a table as shown below.
❖ Degenerated conics
The conics obtained by cutting a plane with a double-napped cone at its vertex are known as degenerating conic sections.
If 1 is the angle between the axis and the generator and
1 is the angle between the axis and the generator and  2 is the angle between the plane and the axis, then, for different conditions of
2 is the angle between the plane and the axis, then, for different conditions of  1 and
1 and  2, we get different conics, which are described with the help of a table as shown below.
2, we get different conics, which are described with the help of a table as shown below.
❖ Circle
A circle is the set of all points in a plane that are equidistant from a fixed point in the plane. The fixed point is called the centre of the circle and the fixed distance from the centre is called the radius of the circle.
❖ Equation of a circle
• with centre at (h, k) and radius r is (x – h)2 + (y – k)2 = r2
• with centre is at origin and radius r is x2 + y2 = r2
❖ Parabola
A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line in the plane).
• The fixed line is called the directrix.
• The fixed point F is called the focus.
• The line through the focus and perpendicular to the directrix is called the axis of the parabola.
• The point of intersection of parabola with the axis is called the vertex of the parabola.
• The line segment that is perpendicular to the axis of the parabola through the focus and whose end points lie on the parabola is called the latus rectum of the parabola.
❖ Standard equations of parabola
❖ If the fixed point lies on the fixed line, then the set of points in the plane that are equidistant from the fixed point and the fixed line is a straight line through the fixed point and perpendicular to the fixed line.
We call this straight line the degenerate case of parabola.
❖ Ellipse
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
• The two fixed points are called the foci.
• The constant, which is the sum of the distances of a point on the ellipse from the two fixed points, is always greater than the distance between the two fixed points.
• The mid-point of the line segment joining the foci is called the centre of the ellipse.
• The line segment through the foci of the ellipse is called the major axis and the line segment through the centre and perpendicular to the major axis is called the minor axis.
• The end points of the major axis are called the vertices of the ellipse.
• The eccentricity of the ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.
• An ellipse is symmetric with respect to both the coordinate axes.
• The line segment that is perpendicular to the major axis of the ellipse through the focus and whose end points lie on the ellipse is called the latus rectum of the ellipse.
.png)
❖ Standard equations of ellipse
❖ Special cases of an ellipse
• When c = 0, i.e., both the foci merge together, then the ellipse becomes a circle.
• When c = a, then b = 0. In such a case, the ellipse reduces to a line segment joining the foci. This means the length of the line segment is 2c.
❖ Hyperbola
A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.
• The two fixed points are called the foci.
• The constant, which is the difference of the distances of a point on the hyperbola from the two fixed points, is always less than the distance between the two fixed points.
• The mid-point of the line segment joining the foci is called the centre of the hyperbola.
• The line through the foci is called the transverse axis and the line through the centre and perpendicular to the transverse axis is called the conjugate axis.
• The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola.
• The eccentricity of the hyperbola is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.
• A hyperbola is symmetric with respect to both the coordinate axes.
• The line segment that is perpendicular to the transverse axis through the focus and whose end points lie on the hyperbola is called the latus rectum of the hyperbola.
❖ Standard equations of hyperbola
❖ A hyperbola having equal lengths of both the axes, i.e., transverse and conjugate (a = b) is called an equilateral hyperbola.Chapter 12: Introduction to Three Dimensional Geometry
❖ Coordinate axes and coordinate planes
• In three-dimensions, the coordinate axes of a rectangular Cartesian coordinate system are three mutually perpendicular lines.
The axes are called x, y, and z-axes.
• The three planes determined by the pair of axes are the coordinate planes, called XY, YZ and ZX-planes.
The three coordinate planes divide the space into eight parts known as octants.
❖ Coordinates of a point
• In three-dimensional geometry, the coordinates of a point P are always written in the form of triplets i.e., (x, y, z).
Here, x, y, and z are the distances from the YZ, ZX and XY-planes.
Also, the coordinates of the origin are (0, 0, 0)
.png)
• The sign of the coordinates of a point determine the octant in which the point lies. The following table shows the signs of the coordinates in the eight octants.
• Coordinates of points lying on different axes
(i) Any point on the x-axis is of the form (x, 0, 0)
(ii) Any point on the y-axis is of the form (0, y, 0)
(iii) Any point on the z-axis is of the form (0, 0, z)
• Coordinates of points lying in different planes
(i) Coordinates of a point in the YZ-plane are of the form (0, y, z)
(ii) Coordinates of a point in the XY-plane are of the form (x, y, 0)
(iii) Coordinates of a point in the ZX-plane are of the form (x, 0, z)
❖ Distance between two points is given by
This is known as the distance formula.
❖ Section formula
The coordinates of point R, which divides the line segment joining two points
• internally in the ratio m: n are
• externally in the ratio m: n are
❖ The coordinates of the mid-point of the line joining the points are .
❖ The coordinates of the centroid of a triangle whose vertices are and x3, y3, z3 areChapter 14: Mathematical Reasoning
❖ A sentence is called a mathematically acceptable statement if it is either true or false, but not both. Statements are denoted by small letters p, q, r, s, etc.
Example: Consider the following sentences:
• “The value of iota is –1.”
It is a statement. Since we know that , the given sentence is false.
• “The number 0 is the smallest whole number.”
It is a statement as this sentence is always true.
• “Do you have internet at your home?”
It is not a statement as it is a question.
❖ Remember
• Sentences involving variable time such as today, tomorrow and yesterday are not statements.
• Sentences involving an exclamation, a question or an order are not statements.
• Sentences involving pronouns such as he or she, unless a particular person is referred to, are not statements.
• Sentences involving pronouns for variable places such as here and there are not statements.
❖ The denial of a statement is called the negation of the statement.
• If p is a statement, then the negation of p is also a statement, and is denoted by ~p, and is read as “not p”.
• While writing the negation of a statement, phrases such as “It is not the case” or “It is false that” are used.
Example:
Write the negation of the following statement:
p: The square root of every positive number is positive.
Solution:
The negation of the given statement can be written as:
The square root of every positive number is not positive.
Or
It is false that the square root of every positive number is positive.
Or
It is not the case that the square root of every positive number is positive.
Or
There exists a positive number whose square root is not positive.
❖ A compound statement is one that is made up of two or more statements.
• Each smaller statement is called the component of the compound statement.
• These components are joined by words such as “And” and “Or”. These are called connectors or connecting words.
Example:
The statement “27 is a multiple of 9 and it is even” is a compound statement.
Its component statements are:
p: “27 is a multiple of 9.”
q: “27 is even.”
Here, the connecting word is “And”.
• A statement with “And” is not always a compound statement.
Example: Water can be prepared by the mixture of hydrogen and oxygen in a certain ratio.
This statement is not a compound statement.
❖ Rules regarding the connector “And”
• The compound statement with the connector “And” is true if all its component statements are true.
• The compound statement with the connector “And” is false if any/both of its component statements is/are false.
❖ Rules regarding the connector “Or”
• A compound statement with the connector “Or” is true when one component statement is true, or both the component statements are true.
• A compound statement with the connector “Or” is false when both the component statements are false.
❖ Types of “Or”
• Exclusive “Or”: A compound statement with the connector “Or” in which either of the component statements may be true, but not both
Example: A student can take home science or painting as his/her additional subject in class XI.
• Inclusive “Or”: A compound statement with the connector “Or” in which either of the component statements or both may be true.
Example: In an equilateral triangle, all the three sides are of equal length or all the three angles are of equal measure.
❖ Some statements may contain special phrases such as “There exists”, “For all”, “For every”. These are called quantifiers.
❖ Implication statement “if-then”: The sentence “if p, then q” says that in the event if p is true, then q must be true. It does not say anything for q when p is false.
• A sentence “if p, then q” can be written in the following ways:
(i) p implies q (denoted by p q)
q)
(ii) p is a sufficient condition for q
(iii) p only if q
(iv) q is a necessary condition for p
(v) ~q implies ~p
❖ Contrapositive and converse of a statement
• The contrapositive of the statement p q is the statement ~q
q is the statement ~q  ~p.
~p.
• The converse of a statement p q is the statement q
q is the statement q  p.
p.
Example: Write the converse and the contrapositive of the following statement:
“If an object is made up of only line segments, then it is a polygon.”
Solution:
The converse of the given statement can be written as follows:
“If an object is a polygon, then it is made up of only line segments.”
The contrapositive of the given statement can be written as follows:
“If an object is not a polygon, then it is not made up of only line segments.”
❖ The equivalent forms of the statement “p if and only if q” (denoted by p q) are as follows:
q) are as follows:
• q if and only if p
• p if and only if q
• p is a necessary and sufficient condition for q and vice-versa
❖ Validating statements
• In order to show that the statement “p and q” is true, the following steps are followed:
1. Show that statement p is true.
2. Show that statement q is true.
• In order to show that the statement “p or q is true”, the following cases are to be considered.
1. Assuming that p is false, show that q must be true.
2. Assuming that q is false, show that p must be true.
• In order to prove the statement “if p, then q’, we need to show that any one of the following cases is true.
1. Assuming that p is true, prove that q must be true. (Direct method)
2. Assuming that q is false, prove that p must be false. (Contrapositive method)
• In order to prove the statement “p if and only if q”, we need to follow the following steps:
1. If p is true, then q is true.
2. If q is true, then p is true.
• Method of contradiction
To check whether a statement p is true, we assume that p is not true, i.e., ~p is true, and then we arrive at some result which contradicts our assumption. Therefore, we conclude that p is true.
This method of proving a given statement to be true is called the contradiction method.
• Using a counter example
In order to disprove a statement, we give an example of the situation where the statement is not valid. Such an example is called a counter example.
In mathematics, counter examples are used for disproving a statement. However, generating examples in favour of a statement does not provide validity to the statement.
Example: The statement “, is true for n = 1, 2, but it is not true for n = 3, 4.
Here, n = 3 and 4 are the counter examples of the given statement. Since the statement is not true for each n ∈ N, the given statement is false. Chapter 15: Statistics
❖ The measures of central tendency, mean, median and mode give us a rough idea where data points are centered.
❖ The dispersion or scatter in a data is measured on the basis of observations and the types of measure of central tendency used. The measures of dispersion are as follows:
• Range
• Quartile deviation
• Mean deviation
• Standard deviation
❖ Range of a series = Maximum value – Minimum value
❖ Mean deviation about mean
• For ungrouped data: , is the mean given by
• For grouped data: , is the mean given by
❖ Mean deviation about median [M.D.(M)]
• For ungrouped data: is the median
• For grouped data: where M is the median and
❖ The mean of the squares of the deviations from mean is called the variance and it is denoted by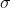 2 .
2 .
❖ Variance of data
• For ungrouped data: (In direct method) or (In shortcut method), where is the mean.
• For discrete frequency distribution: (In direct method) or (In shortcut method), where is the mean and.
is the mean and.
• For continuous frequency distribution: or (In direct method) or (In shortcut method), where
xi = class marks of the class intervals, = mean,
= mean,  , h = width of the class intervals, , where A is the assumed mean.
, h = width of the class intervals, , where A is the assumed mean.
❖ Adding (or subtracting) a positive number to (or from) each observation does not affect the variance.
❖ If each observation is multiplied with a constant k, then the variance of the resulting observations becomes k2 times the original variance.
❖ Standard deviation is the square root of variance and it is denoted by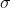 . This means:
. This means:
❖ Coefficient of variation
The measure of variability, which is independent of units, is called the coefficient of variation. The coefficient of variation (C.V.) is defined as
Where,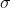 and are standard deviation and mean of the data respectively.
and are standard deviation and mean of the data respectively.
• For comparing the variability or dispersion of two series, we first calculate the C.Vs of each series.
The series having higher C.V. is said to be more variable than the other and the series having lower C.V. is said to be more consistent than the other.
• For two series with equal mean values, the series with greater standard deviation (or variance) is more variable or dispersed than the other.
Also, the series with lower value of standard deviation (or variance) is said to be more consistent or less scattered than the other.Chapter 16: Probability
❖ An experiment is called a random experiment if it satisfies the following two conditions:
• It has more than one possible outcome
• It is not possible to predict the outcome in advance
❖ A possible result of a random experiment is called its outcome.
❖ The set of all possible outcomes of a random experiment is called the sample space associated with the experiment. It is denoted by S.
Each element of the sample space i.e., each outcome of the random experiment is called the sample point.
❖ Any subset (E) of a sample space is called an event.
• The event (E) of a sample space (S) is said to have occurred if the outcome ( ) of the experiment is such that
) of the experiment is such that  ∈ E.
∈ E.
• If the outcome ( ) is such that
) is such that  ∉ E, we say that the event (E) has not occurred.
∉ E, we say that the event (E) has not occurred.
❖ Types of events
• Impossible event: An empty set (ϕ) is called an impossible event.
• Sure event: The whole sample space (S) is called a sure event.
• Simple event: If an event (E) has only one sample point of a sample space, then it is called a simple (or elementary) event.
In a sample space containing n distinct elements, there are exactly n simple events.
• Compound event: If an event has more than one sample point, it is called a compound event.
Example: Consider an experiment of selecting numbers from first 50 natural numbers, then the sample space (S) is given as
S = {1, 2, 3, 4, … 49, 50}
In this case,
(i) The event “Getting a number that is a multiple of both 7 and 9” is an impossible event as there is no outcome related to it.
(ii) The event “Getting a perfect square that is more than 40” is a simple event since E = {49}.
(iii) The event “Getting an odd multiple of 13” is a compound event since E = {13, 39}.
❖ Algebra of events
• Complementary event: For every event A, there corresponds another event Aʹ called the complementary event to A. It is also called the event ‘not A’.
Aʹ = { :
:  ∈ S and
∈ S and  ∉ A} = S – A.
∉ A} = S – A.
• Event ‘A or B’: When sets A and B are two events associated with a sample space, then the set A ⋃ B is the event ‘either A or B or both’.
That is, event ‘A or B’ = A ⋃ B = { :
:  ∈ A or
∈ A or  ∈ B}
∈ B}
• Event ‘A and B’: When sets A and B are two events associated with a sample space, then the set A ⋂ B is the event ‘A and B’.
That is, event ‘A and B’ = A ⋂ B = { :
:  ∈ A and
∈ A and  ∈ B}
∈ B}
• Event ‘A but not B’: When sets A and B are two events associated with a sample space, then the set A – B is the event ‘A but not B’.
That is, event ‘A but not B’ = A – B = A ⋂ Bʹ = { :
:  ∈ A and
∈ A and  ∉ B}
∉ B}
Example:
Consider the experiment of tossing 2 coins. Let A be the event ‘getting at least one head’ and B be the event ‘getting exactly two heads’. Find the sets representing the events
(i) complement of ‘A or B’
(ii) A and B
(iii) A but not B
Solution:
Here, S = {HH, HT, TH, TT}
A = {HH, HT, TH}, B = {HH}
(i) A or B = A ⋃ B = {HH, HT, TH}
Hence, complement of ‘A or B’ = (A or B)ʹ = (A ⋃ B)ʹ = {TT}
(ii) A and B = A ⋂ B = {HH}
(iii) A but not B = A – B = {HT, TH}
❖ Two events, A and B, are called mutually exclusive events if the occurrence of any one of them excludes the occurrence of the other event i.e., if they cannot occur simultaneously.
In this case, sets A and B are disjoint i.e., A ⋂ B = ϕ
❖ If E1, E2, … En are n events of a sample space S, and if
E1 ⋃ E2 ⋃ …. ⋃ En = , then
E1, E2 … En are called mutually exhaustive events.
In other words, at least one of E1, E2 … En necessarily occurs whenever the experiment is performed.
❖ The events E1, E2, … En, i.e., n events of a sample space (S) are called mutually exclusive and exhaustive events if
• Ei ⋂ Ej = ϕ for i ≠ j i.e., events Ei and Ej are pairwise disjoint, and
•
❖ The number P ( i) i.e., the probability of the outcome
i) i.e., the probability of the outcome  i, is such that
i, is such that
• 0 ≤ P( i) ≤ 1
i) ≤ 1
• ΣP( i) = 1 for all
i) = 1 for all  i ∈ S
i ∈ S
• For any event A, P(A) = ΣP( i) for all
i) for all  i ∈ A
i ∈ A
❖ For a finite sample space, S, with equally likely outcomes, the probability of an event A is denoted as P (A) and it is given by
,
Where, n(A) = Number of elements in set A and n(S) = Number of elements in set S
❖ If A and B are two events, then P (A ⋃ B) = P (A) + P (B) – P (A ⋂ B)
❖ If A and B are mutually exclusive events, then P (A ⋃ B) = P (A) + P (B)
❖ If A is any event, then P (A′) = 1 – P (A)Chapter 13: Limits and Derivatives
❖ Limit of a function
• is the expected value of f at x = a, given the values of f near x to the left of a. This value is called the left hand limit of f(x) at a.
• is the expected value of f at x = a, given the values of f near x to the right of a. This value is called the right hand limit of f(x) at a.
• If the right and left hand limits coincide, we call that common value the limit of f(x) at x = a, and denote it by .
• For a function f and a real number a, and f(a) may not be the same.
❖ Algebra of limits
Let f and g be two functions such that both exist. Then,
•
•
• , where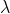 is a constant
is a constant
•
❖ Some standard limits
• For a polynomial function f(x), .
• If f(x) is a rational function of the form , where g(x) and h(x) are polynomial functions, such that h(x) ≠ 0, then .
• , where n is a positive integer or any rational number and a is positive
•
•
❖ Let f and g be two real-valued functions with the same domain, such that f(x) ≤ g(x) for all x in the domain of definition.
For some a, if both exist, then .
❖ Sandwich theorem
Let f, g, and h be real functions such that f(x) ≤ g(x) ≤ h(x) for all x in the common domain of definition. For some real number a, if .
❖ Derivatives
• Suppose f is a real-valued function and a is a point in its domain of definition. The derivative of f at a [denoted by f′(a)] is defined as
, provided the limit exists.
Derivative of f(x) at a is denoted by f′(a).
• Suppose f is a real-valued function. The derivative of f {denoted by f'(x) or} is defined as
, provided the limit exists.
This definition of derivative is called the first principle of derivative.
❖ Algebra of derivatives of functions
For the functions u and v (provided uʹ and vʹ are defined in a common domain),
•
•
•
❖ Some standard derivatives
• for any positive integer n
•
•
•
•
❖ A set is a well-defined collection of objects.
• Example: The collection of all rational numbers less than 10 is a set whereas the collection of all the brilliant students in a class is not a set.
• Sets are usually denoted by capital letters A, B, S, etc.
• The elements of a set are usually denoted by small letters a, b, t, u, etc.
❖ If x is an element of a set S, then we say that “x belongs to S”. Mathematically, we write it as x ∈ S. If y is not an element of a set S, then we say that “y does not belong to S”.
Mathematically, we write it as y ∈ S.
❖ Methods for representing a set
• Roster or tabular form: In this form, all the elements of a set are listed, separated by commas and enclosed within braces { }.
In this form, the order in which the elements are listed is immaterial, and the elements are not repeated.
Example: The set of letters forming the word ‘TEST’ is {T, E, S}.
• Set-builder form: In this form all the elements of a set possess a single common property which is not possessed by any element outside the set.
Example: The set {2, –2} can be written in the set-builder form as {x : x is an integer and x2 – 4 = 0}.
❖ Types of sets
• A set which does not contain any element is called an empty set or a null set or a void set. It is denoted by the symbol ϕ or { }.
Example: The set {x : x ∈ N, x is an even number and 8 < x < 10} is an empty set.
• A set which is empty or consists of a definite number of elements is called finite; otherwise, the set is called infinite.
Example: The set {x : x ∈ N and x is a square number} is an infinite set. The set {x : x ∈
N and x2 – 2x – 3 = 0} is a finite set as it is equal to {–1, 3}.
❖ All infinite sets cannot be described in the roster form.
For example, the set of rational numbers cannot be described in this form. This is because the elements of this set do not follow any particular pattern.
❖ Two sets A and B are said to be equal if they have exactly the same elements and we write A = B; otherwise, the sets are said to be unequal and we write A ≠ B.
Example: The sets A = {x :x ∈ N and (x – 1)(x + 4) = 0} and B = {–4, 1} are equal sets.
❖ A set does not change if one or more elements of the set are repeated.
Example: The sets A = {E, L, E, M, E, N, T, S} and B = {E, L, M, N, T, S} are equal since each element of A is in B, and vice-versa.
❖ Subsets
• A set A is said to be a subset of a set B if every element of A is also an element of B and we write A ⊂ B.
In other words, A ⊂ B if a ∈ A
• A ⊂ B and B ⊂ A
• An empty set is a subset of every set.
• Every set is a subset of itself.
• If A ⊂ B and A ≠ B, then A is called a proper subset of B, and B is called a superset of A.
❖ If a set has only one element, then it is called a singleton set.
Example: A = {–17} is a singleton set.
❖ Intervals as subsets of R
Let a, b ∈ R and a < b. Then,
• {y : a < y < b} is called an open interval and is denoted by (a, b).
In the open interval (a, b), all the points between a and b belong to the open interval (a, b), but a, b themselves do not belong to this interval.
• {y : a ≤ y ≤ b}is called a closed interval and is denoted by [a, b]. In this interval, all the points between a and b as well as the points a and b are included.
• [a, b) = {y : a ≤ y < b}is an open interval from a to b, including a, but excluding b.
• (a, b] = {y : a < y ≤ b}is an open interval from a to b, including b, but excluding a.
❖ Power set
• The collection of all subsets of a set A is called the power set of A. It is denoted by P(A).
• If A is a set with n(A) = m, then n[P(A)] = 2m.
❖ Venn diagrams
Most of the relationships between sets can be represented by means of diagrams known as Venn diagrams.
❖ A universal set is the super set of all sets under consideration and is denoted by U.
❖ Union of sets
• The union of two sets A and B is the set which contains all those elements which are only in A, only in B and in both A and B, and this set is denoted by ‘A ⋃ B’.
A ⋃ B = {x: x ∈ A or x ∈ B}
• Properties of union of sets
(i) A⋃B = B⋃A (Commutative Law)
(ii) (A⋃B) ⋃C = A⋃(B⋃C) (Associative Law)
(iii) A⋃ϕ = A (ϕ is the identity of ⋃)
(iv) A⋃A = A (Idempotent Law)
(v) U⋃A = U (Law of U)
❖ Intersection of sets
• The intersection of two sets A and B is the set of all those elements which belong to both A and B. It is denoted by ‘A ⋂ B’.
• Properties of intersection of sets
(i) A ⋂ B = B ⋂ A (Commutative Law)
(ii) (A ⋂ B) ⋂ C = A ⋂(B ⋂ C) (Associative Law)
(iii) ϕ ⋂ A = ϕ (Law of ϕ)
(iv) U ⋂ A = A (Law of U)
(v) A ⋂ A = A (Idempotent Law)
(vi) A ⋂ (B ⋃ C) = (A ⋂ B) ⋃ (A ⋂ C) (Distributive law of ⋂ on ⋃)
(vii) A ⋃ (B ⋂ C) = (A ⋃ B) ⋂ (A ⋃ C)
❖ Difference of sets
• The difference between the sets A and B (i.e., A – B, in this order) is the set of the elements which belong to A, but not to B.
A – B = {x: x ∈ A and x ∉ B}
• Properties of operation of difference of sets
(i) A – B =A – (A ⋂ B)
(ii) For A ≠ B, A – B ≠ B – A
(iii) For A = B, A – B = B – A = ϕ
(iv) For B = ϕ, A – B = A and B – A = ϕ
(v) A – U = ϕ
(vi) For A ⊂ B, A – B = ϕ; for this reason, A – U = ϕ
❖ The sets A – B, A ⋂ B and B – A are mutually disjoint sets, i.e., the intersection of any of these two sets is a null set.
.png)
❖ Complement of a set
• If U is a universal set and A is a subset of U, then the complements of A are denoted by the set A'. This is the set of all element of U which are not the elements of A.
A' = {x: x ∈U and x∉ A} = U – A
A' is also the subset of U
• Properties of complement of a set
(i) (A')' =A
(ii) A ⋃ A' = U
(iii) A ⋂ A' = ϕ
(iv) ϕ' = U and U' = ϕ
• De Morgan’s laws
For any sets A and B,
(i) (A ⋃ B)' = A' ⋂ B'
(ii) (A ⋂ B)' = A' ⋃ B'
❖ If A and B are finite sets, such that A ⋂ B = ϕ, then n(A ⋃ B) = n(A) + n(B)
❖ If A and B are finite sets, such that A ⋂ B ≠ ϕ, then, n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B)
If A, B and C are finite sets, then n(A ⋃ B ⋃ C) = n(A) + n(B) + n(C) – n (A ⋂ B) – n(B ⋂ C) – n(A ⋂ C) + n(A ⋂ B ⋂ C)Chapter 2: Relations and Functions
❖ Cartesian product of sets
• Two non-empty sets P and Q are given. The Cartesian product P × Q is the set of all ordered pairs of elements from P and Q, i.e.,
P × Q = {(p,q): p ∈ P and q ∈Q}
• If either P or Q is a null set, then P × Q will also be a null set, i.e., P × Q = ϕ.
In general, if A is any set, then A × ϕ = ϕ.
• Two ordered pairs are equal if and only if the corresponding first elements are equal and the second elements are also equal. In other words, if (a, b) = (x, y), then a = x and b = y.
❖ For any two sets A and B
• A × B ≠ B × A
• If n(A) = p, n(B) = q, then n(A × B) = pq
• If A and B are non-empty sets and either A or B is an infinite set, then so is the case with A × B
❖ A × A × A = {(a, b, c) : a, b, c ∈ A}. Here, (a, b, c) is called an ordered triplet.
❖ Relation
A relation R from a set A to a set B is a subset of the Cartesian product A × B, obtained by describing a relationship between the first element x and the second element y of the ordered pairs (x, y) in A × B.
• The image of an element x under a relation R is y, where x, y ∈ R.
• The set of all the first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R.
• The set of all the second elements in a relation R from a set A to a set B is called the range of the relation R. The whole set B is called the co-domain of the relation R.
Range ⊆ Co-domain
❖ The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A × B.
If n(A) = p and n(B) = q, then n(A × B) = pq and the total number of relations is 2pq.
❖ Functions
A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.
In other words, a function f is a relation from a non-empty set A to another non-empty set B, such that the domain of f is A and no two distinct ordered pairs in f have the same first element.
• The function f from A to B is denoted by f : A → B. Here, A is the domain and B is the co-domain of f.
• If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f, and a is called the pre-image of b under f.
• A function having either R (real numbers) or one of its subsets as its range is called a real-valued function. Further, if its domain is also either R or a subset of R, it is called a real function.
❖ Types of functions
• Identity function: The function f: R → R defined by y = f(x) = c, for each x ∈ R, is called the identity function.
Here, R is the domain and range of f.
• Constant function: The function f: R → R defined by y = f(x) = c, for each x ∈ R, where c is a constant, is a constant function.
Here, the domain of f is R and its range is {c}.
• Polynomial function: A function f: R → R is said to be a polynomial function if for each x ∈ R, , where n is a non-negative integer and .
• Rational function: The functions of the type , where f(x) and g(x) are polynomial functions of x defined in a domain and where g(x) ≠ 0, are called rational functions.
• Modulus function: The function f: R → R defined by f(x) = |x|, for each x ∈ R, is called the modulus function.
In other words,
• Signum function: The function f: R → R defined by
is called the signum function. Its domain is R and its range is the set {–1, 0, 1}.
• Greatest Integer function: The function f: R → R defined by f(x) = [x], x ∈ R, assuming the value of the greatest integer less than or equal to x, is called the greatest integer function.
• Linear function: The function f defined by f(x) = mx + c, for x ∈ R, where m and c are constants, is called the linear function. Here, R is the domain and range of f.
❖ Algebra of functions
For functions f: X → R and g: X → R, we define
• (f + g): X → R by (f + g) (x) = f(x) + g (x), x ∈ X
• (f – g): X → R by (f – g) (x) = f(x) – g (x) x ∈ X
• (fg): X → R by (fg) (x) = f(x) . g(x), x ∈ X
• (af): X → R by (α f)(x) = α f(x), x ∈ X and α is a real number
• , x ∈ X and g(x) ≠ 0.Chapter 3: Trigonometric Functions
❖ Consider a circle of radius r having an arc of length l that subtends an angle of θ radians.
Then, l = rθ.
❖ Relation between radian and degree measure
Radian measure =
❖ A degree is divided into 60 minutes and a minute is divided into 60 seconds. One sixtieth of a degree is called a minute, written as 1', and one sixtieth of a minute is called a second, written as 11".
Thus, 10 = 60' and 1' = 60"
❖ Domain and range of trigonometric functions
| Trigonometric function | Domain | Range |
| sin x | R | [–1, 1] |
| cos x | R | [–1, 1] |
| tan x | R | |
| cot x | R – {x : x = nπ, n ∈Z} | R |
| sec x | R – [–1, 1] | |
| cosec x | R – {x : x = nπ, n ∈ Z} | R – [–1, 1] |
❖ Signs of trigonometric functions in different quadrants
| Trigonometric
function
|
Quadrant I | Quadrant II | Quadrant III | Quadrant IV |
| sin x | + ve (Increases from 0 to 1) | + ve (Decreases from 1 to 0) | – ve (Decreases from 0 to –1) | – ve (Increases from –1 to 0) |
| cos x | + ve (Decreases from 1 to 0) | – ve (Decreases from 0 to –1) | – ve (Increases from –1 to 0) | + ve (Increases from 0 to 1) |
| tan x | + ve (Increases from 0 to ∞) | – ve (Increases from –∞ to 0) | + ve (Increases from 0 to ∞) | – ve (Increases from –∞ to 0) |
| cot x | + ve (Decreases from ∞ to 0) | – ve (Decreases from 0 to –∞) | + ve (Decreases from ∞ to 0) | – ve (Decreases from 0 to –∞) |
| sec x | + ve (Increases from 1 to ∞) | – ve (Increases from –∞ to –1) | – ve (Decreases from –1 to –∞) | + ve (Decreases from ∞ to 1) |
| cosec x | + ve (Decreases from ∞ to 1) | + ve (Increases from 1 to ∞) | – ve (Increases from –∞ to –1) | – ve (Decreases from –1 to –∞) |
❖ Trigonometric identities
•
•
•
•
• cos2 x + sin2 x = 1
• 1 + tan2 x = sec2 x
• 1 + cot2 x = cosec2x
❖ Trigonometric ratios of allied angles
• sin (–x) = – sin x
• cos (–x) = cos x
•
•
•
•
• cos (π – x) = – cos x
• sin (π – x) = sin x
• cos (π + x) = – cos x
• sin (π + x) = – sin x
• cos (2π – x) = cos x
• sin (2π – x) = – sin x
• cos (2nπ + x) = cos x, n ∈ Z
• sin (2nπ + x) = sin x, n ∈ Z
❖ Sum and difference of two angles
• sin (x + y) = sin x cos y + cos x sin y
• cos (x + y) = cos x cos y – sin x sin y
• sin (x – y) = sin x cos y – cos x sin y
• cos (x – y) = cos x cos y + sin x sin y
• If none of the angles x, y and (x
• If none of the angles x, y and (x
❖ Trigonometric ratios of multiple angles
•
•
•
• sin 3x = 3 sin x – 4 sin3 x
• cos 3x = 4 cos3x – 3 cos x
•
❖ Some more trigonometric identities
•
•
•
•
• 2 cos x cosy = cos (x + y) + cos (x – y)
• –2 sin x sin y = cos (x + y) – cos (x – y)
• 2 sin x cos y = sin (x + y) + sin (x – y)
• 2 cos x sin y = sin (x + y) – sin (x – y)
❖ General solutions of trigonometric equations
•
•
•
•
• Chapter 4: Principle of Mathematical Induction
❖ There are some mathematical statements or results that are formulated in terms of n, where n is a positive integer. To prove such statements, the well-suited principle that is used, based on the specific technique, is known as the principle of mathematical induction.
❖To prove a given statement in terms of n, we assume the statement to be P(n).
1. Thereafter, we examine the correctness of the statement for n = 1 i.e., for P(1) to be true.
2. Then, assuming that the statement is true for n = k, where k is a positive integer, we prove that the statement is true for n = k + 1 i.e., the truth of P(k) implies the truth of P
(k + 1). Then, we say that P(n) is true for all natural numbers n.
Example: For all n∈N, prove that
Solution:
Let the given statement be P(n), i.e.,
For n = 1, , which is true.
Now, assume that P(x) is true for some positive integer k. This means
We shall now prove that P(k + 1) is also true.
Now, we have
Thus, P(k + 1) is true whenever P(k) is true. Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.Chapter 5: Complex Numbers and Quadratic Equations
❖ A number of the form a + ib, where a and b are real numbers and , is defined as a complex number.
• For the complex numbers z = a + ib, a is called the real part (denoted by Re z) and b is called the imaginary part (denoted by Im z) of the complex number z.
❖ Two complex numbers z1 = a + ib and z2 = c + id are equal if a = c and b = d.
❖ Addition of complex numbers
• Let z1 = a + ib and z2 = c + id be any two complex numbers. The sum is defined as z1 + z2 = (a + c) + i (b + d).
• Properties of addition of complex numbers
(i) Closure law: Sum of two complex numbers is also a complex number.
(ii) Commutative law: For two complex numbers z1 and z2, z1 + z2 = z2 + z1
(iii) Associative law: For any three complex numbers z1, z2 and z3, (z1 + z2) + z3 = z1 + (z2 + z3)
(iv) Existence of additive identity: There exists a complex number 0 + i0 (denoted by 0), called the additive identity or zero complex number, such that for every complex number z, z + 0 = z
(v) Existence of additive inverse: For every complex number z = a+ ib, there exists a complex number –a + i(–b) [denoted by –z], called the additive inverse or negative of z, such that z + (–z) = 0
❖ Given any two complex numbers z1, and z2, the difference z1 - z2 is defined as z1 - z2 = z1 + (– z2)
❖ Multiplication of complex numbers
• For two complex numbers z1 and z2, such that z1 = a + ib and z2 = c + id, the multiplication is defined as z1 z2 = (ac - bd) + i(ad + bc).
• Properties of multiplication of complex numbers
(i) Closure law: The product of two complex numbers is also a complex number.
(ii) Commutative law: For any two complex numbers z1 and z2, z1z2 = z2z1.
(iii) Associative law: For any three complex numbers z1, z2 and z3, (z1z2) z3 = z1 (z2z3)
(iv) Existence of multiplicative identity: There exist a complex number 1 + i 0 (denoted as 1), called the multiplicative identity, such that for every complex numbers z, z.1 = z
(v) Existence of multiplicative inverse: For every non-zero complex number z = a + ib a ≠ 0, b ≠ 0, we have the complex number
(denoted by or z–1), called the multiplicative inverse of z, such that=1
(vi) Distributive law: For any three complex numbers z1, z2 and z3, z1 (z2 + z3) = z1z2 + z1z3
(z1 + z2) z3 = z1z3 + z2z3
❖ Given any two complex number z1 and z2, where z2 ≠ 0, the quotient is defined as
❖ Powers of i
For any integer
❖ If a and b are negative real numbers, then .
❖ Identities for complex numbers
For two complex numbers z1 and z2
•
•
•
•
•
❖ Modulus and conjugate of complex numbers
• The modulus of a complex number z = a + ib, is denoted by |z|, and is defined as the non-negative real number, i.e., .
• The conjugate of a complex number z = a + ib, is denoted by , and is defined as the complex number a – ib, i.e., .
❖ Properties of modulus and conjugate of complex numbers
For any three complex numbers z, z1, z2,
•
•
•
•
•
•
❖ The polar form of the complex number z = x + iy, is r(cos
The value of
Example: Represent the complex number in polar form.
Solution:
Let
By squaring and adding them, we have
Thus,
Thus, the required polar form is 2.
❖ A polynomial equation of n degree has n roots.
❖ The solutions of the quadratic equation ax2 + bx + c = 0, where a, b, c ∈ R, a ≠ 0 and b2 – 4ac < 0, are given by .Chapter 6: Linear Inequalities
❖ Two real numbers or two algebraic expressions related by the symbol ‘<’, ‘>’, ‘≤’ or ‘≥’ form an inequality.
❖ The solution of an inequality in one variable is a value of the variable which makes it a true statement.
❖ Solution of linear inequalities in one variable
• Solving an inequality algebraically
(i) Equal numbers may be added to or subtracted from both sides of an inequality without affecting the sign of the inequality.
(ii) Both sides of an inequality can be multiplied with or divided by the same positive number. But when both sides are multiplied with or divided by a negative number, the sign of inequality is reversed.
• Graphical representation of Solution
(i) To represent x < a (or x > a) on a number line, encircle the number a, and darken the line to the left (or the right) of a.
(ii) To represent x ≤ a (or x ≥ a) on a number line, encircle the number a, and darken the line to the left (or the right) of a.
Example:
Solve 5(x – 3) ≤ 2x + 9
Solution:
5(x – 3) ≤ 2x + 9
Thus, the solution of the given inequality can be represented on the number line as shown below:

❖ Graphical solution of linear inequalities in two variables
• The solution region of a system of inequalities is the region which satisfies all the given inequalities in the system simultaneously.
• In order to identify the half plane represented by an inequality, it is sufficient to take any point (a, b) (not on the line) and check whether it satisfies the inequality or not.
If it satisfies, then the inequality represents the half plane containing the point and we shade this region.
If not, then the inequality represents the half plane which does not contain the point. For convenience, the point (0, 0) is preferred.
• In an inequality of the type ax + by ≥ c or ax + by ≤ c, the points on the line ax + by = c are to be included in the solution region. So, we darken the line in the solution region.
• In an inequality of the type ax + by > c or ax + by < c, the points on the line ax + by = c are not to be included in the solution region. So, we draw a broken or dotted line in the solution region.
Example:
Solve the following system of linear inequalities graphically: 2x – y ≤ 4, x < 2
Solution:
The given linear inequalities are
2x – y ≤ 4 ...(i)
x < 2 ...(ii)
The graphs of the lines 2x – y = 4 and x = 2 are drawn in the figure below.
.png)
Inequality (i) represents the region on the left of the line 2x – y = 4 (including the line 2x – y = 4). Inequality (ii) represents the region on the left of the line x = 2 (excluding the line x = 2).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region, including the points on the line 2x – y = 4.Chapter 7: Permutations and Combinations
❖ If an event occurs in m different ways, following which another event occurs in n different ways, then the total number of occurrence of the events in the given order is m × n.
This is called the fundamental principle of counting.
❖ A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.
❖ Factorial notation
• The notation n! represents the product of the first n natural numbers, i.e., n! = 1 × 2 × 3 × ………× n
• 0! = 1
❖ The number of permutations of n different things taken r at a time,
• When repetition is not allowed, is denoted by nPr and is given by .
• When repetition is allowed, is nr.
❖ Permutations when all the objects are not distinct
• The number of permutations of n objects, when p objects are of the same kind and the rest are all different, is .
• The number of permutations of no objects, where p1 objects are of one kind, p2 are of the second kind , …………. , pk are of the kth kind and the rest, if any, are of different kinds, is .
❖ A combination is different selections of a number of objects taken a few or all at a time, irrespective of their arrangements.
❖ The number of combinations of n different things taken r at a time is denoted by nCr, which is given by
❖ Properties of nCr
•
•
• Chapter 8: Binomial Theorem
❖ The coefficients of the expansions of a binomial are arranged in an array. This array is called Pascal’s triangle. It can be written as:
| Index | Coefficient(s) |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 |
❖ Binomial theorem for any positive integer
• The expansion of a binomial for any positive integral n is as follows:
• Some points about Binomial Theorem
(i) The notation stands for
Hence, the binomial theorem can also be stated as follows:
(ii) The coefficients of nCk occurring in the binomial theorem are known as binomial coefficients
(iii) In the expansion of (a + b)n, there are (n + 1) terms i.e., one more than the index.
(iv) In the successive terms of the expansion of (a + b)n, the index of a goes on decreasing by unity, starting with n in the first term and ending with 0 in the last term. Also, the index of b increases by unity, starting with 0 in the first term and ending with n in the last term.
(v) In every term of the expansion, the sum of the indices of a and b is n.
❖ In the binomial expansion of (a + b)n, taking a = x and b = – y, we have
❖ The (r + 1)th term (denoted by Tr + 1) is known as the general term of the expansion (a + b)n and it is given by
❖ Middle term in the expansion of (a + b)n
• If n is even, then the number of terms in the expansion will be n + 1. Since n is even, n + 1 is odd. Therefore, the middle term is term.
• If n is odd, then n + 1 is even. So, there will be two middle terms in the expansion. They are term and term.Chapter 9: Sequences and Series
❖ A sequence is an arrangement of numbers in definite order according to some rule.
• A sequence may be defined as a function whose domain is the set of natural numbers or some subset of the type {1, 2, 3… k}.
• A sequence containing finite number of terms is called a finite sequence, whereas a sequence containing infinite number of terms is called an infinite sequence.
❖ The general form of a sequence is a1, a2, a3, … an –1 , an, …
• a1, a2 … etc. are called the terms of the sequence.
• The nth term of the sequence, an, is called the general term of the sequence.
❖ An arrangement of numbers such as 1, 2, 4, 6, 10 … has no visible pattern. However, the sequence is generated by the recurrence relation given by
This sequence is called the Fibonacci sequence.
❖ Let a1, a2,… an –1,… be a given sequence. Accordingly, the sum of this sequence is given by the expression a1+ a2+…+an +...
This is called the series associated with the given sequence.
• The series is finite or infinite according as the given sequence.
• A series is usually represented in a compact form using sigma notation (
This means the series a1+ a2+...+ an –1+ an can be written as
❖ Arithmetic progression
The sequence a1, a2,… an … is called an arithmetic sequence or an arithmetic progression (A.P.) if. an +1 = an + d, n ∈N.
Here, a1is called the first term and d is called the common difference of the A.P.
In standard form, the A.P. is written as a, a + d, a + 2d…
• The nth or the general term of an A.P. is given by an = a + (n – 1) d.
• If a is the first term, d is the common difference, l is the last term and n is the number of terms, then l = a + (n – 1) d.
• The sum of n terms of an A.P. (denoted by Sn) is given by
❖ Properties of an A.P.
• If a constant is added or subtracted or multiplied to each term of an A.P., then the resulting sequence is also an A.P.
• If each term of an A.P. is multiplied or divided by a non-zero constant, then the resulting sequence is also an A.P.
❖ Arithmetic mean
• For any two numbers a and b, we can insert a number A between them such that a, A, b is an A.P.
Here, A is called the arithmetic mean (A.M.) of numbers a and b and .
• Let A1, A2… An be n numbers between a and b such that a, A1, A2,…, An, b is an A.P.
Accordingly, common difference (d) is given by .
The numbers A1, A2… An are given as follows:
❖ Geometric progression
A sequence is said to be a geometric progression (G.P.) if the ratio of any term to its preceding term is the same throughout. This constant factor is called the common ratio and it is denoted by r.
In standard form, the G.P. is written as a, ar, ar2… where, a is the first term and r is the common ratio.
• The nth term (or general term) of a G.P. is given by an = ar n – 1
• The sum of n terms (Sn) of a G.P. is given by
❖ Geometric mean
• For any two positive numbers a and b, we can insert a number G between them such that a, G, b is a G.P. G is called a geometric mean (G.M.) and is given by
• Let G1, G2, …,Gn be n numbers between positive numbers a and b such that a, G1, G2, …, Gn, b is a G.P. Common ratio of G.P.,
Therefore, G1= ar, G2 = ar2,…, Gn = arn
❖ Let A and G be the respective A.M. and G.M. of two given positive real numbers a and b.
•
• A ≥ G
❖ Sum of n-terms of some special series
• Sum of first n natural numbers
• Sum of squares of the first n natural numbers
• Sum of cubes of the first n natural numbers
Chapter 10: Straight Lines
❖ Slope of a line
If
.png)
The slope of a line is denoted by m.
Thus, m = tan
• The slope of a line whose inclination is 90º is not defined. Hence, the slope of the vertical line (y-axis) is undefined.
• The slope of the horizontal line (x-axis) is zero.
❖ The slope (m) of a non-vertical line passing through the points (x1, y1) and (x2, y2) is given by .
❖ Suppose l1 and l2 are non-vertical lines having slopes m1 and m2 respectively
• l1 is parallel to l2 if and only if m1 = m2, i.e., their slopes are equal.
• l1 is perpendicular to l2 if and only if m1m2 = –1, i.e., the product of their slopes is –1.
• An acute angle,
❖ Three points A, B and C are collinear if and only if
Slope of AB = Slope of BC
❖ Horizontal and vertical lines
• The equation of a horizontal line at distance a from the x-axis is either y = a (above x-axis) or y = – a (below y-axis).
• The equation of a vertical line at distance b from the y-axis is either x = b (right of y-axis) or x = – b (left of y-axis).
❖ Point-slope form of a line
The point (x, y) lies on the line with slope m through the fixed point (x0, y0) if and only if its coordinates satisfy the equation. This means y – y0 = m (x – x0).
❖ Two-point form of a line
The equation of the line passing through the points (x1, y1) and (x2, y2) is given by
.
❖ Slope-intercept form of a line
• The equation of the line, with slope m, which makes y-intercept c is given by y = mx + c.
• The equation of the line, with slope m, which makes x-intercept d is given by y = m(x – d).
❖ Intercept form of a line
The equation of the line making intercepts a and b on x-axis and y-axis respectively is
❖ Normal form of a line
The equation of the line at normal distance p from the origin and angle
❖ Any equation of the form Ax + By + C = 0, where A and B are not zero simultaneously is called the general linear equation or general equation of line.
❖ The perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is
.
❖ The distance (d) between two parallel lines i.e., Ax + By + C1 = 0 and Ax + By + C2 = 0 is given by
Chapter 11: Conic Sections
❖ Conic sections or conics are the curves that are obtained by intersecting a plane with a double-napped right circular cone. Circles, ellipses, parabolas and hyperbolas are examples of conic sections.
❖ A double-napped cone can be obtained by rotating a line (let us say m) about a fixed vertical line (let us say l).
.png)
Here, the fixed line l is called the axis of the cone and m is called the generator of the cone. The intersection (V) of l and m is called the vertex of the cone.
❖ Different conics formed by intersecting a plane and a double-napped cone
If
| Condition | Conic Formed | Figure |
| A circle | .png) |
|
| An ellipse | .png) |
|
| A parabola | .png) |
|
| 0 < |
A hyperbola | .png) |
❖ Degenerated conics
The conics obtained by cutting a plane with a double-napped cone at its vertex are known as degenerating conic sections.
If
| Condition | Conic Formed | Figure |
| A point | .png) |
|
| A straight line | .png) |
|
| 0 ≤ |
A hyperbola | .png) |
❖ Circle
A circle is the set of all points in a plane that are equidistant from a fixed point in the plane. The fixed point is called the centre of the circle and the fixed distance from the centre is called the radius of the circle.
❖ Equation of a circle
• with centre at (h, k) and radius r is (x – h)2 + (y – k)2 = r2
• with centre is at origin and radius r is x2 + y2 = r2
❖ Parabola
A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not on the line in the plane).
• The fixed line is called the directrix.
• The fixed point F is called the focus.
• The line through the focus and perpendicular to the directrix is called the axis of the parabola.
• The point of intersection of parabola with the axis is called the vertex of the parabola.
• The line segment that is perpendicular to the axis of the parabola through the focus and whose end points lie on the parabola is called the latus rectum of the parabola.
❖ Standard equations of parabola
.png) |
Open Towards | Right |
| Standard Equation | y2 = 4ax, a > 0 | |
| Coordinates of Focus | (a, 0) | |
| Coordinates of Vertex | (0, 0) | |
| Equation of Directrix | x = –a | |
| Length of Latus Rectum | 4a | |
| Axis of Parabola | Positive x-axis |
.png) |
Open Towards | Left |
| Standard Equation | y2 = –4ax, a > 0 | |
| Coordinates of Focus | (–a, 0) | |
| Coordinates of Vertex | (0, 0) | |
| Equation of Directrix | x = a | |
| Length of Latus Rectum | 4a | |
| Axis of Parabola | Negative x-axis |
.png) |
Open Towards | Upward |
| Standard Equation | x2 = 4ay, a > 0 | |
| Coordinates of Focus | (0, a) | |
| Coordinates of Vertex | (0, 0) | |
| Equation of Directrix | y = –a | |
| Length of Latus Rectum | 4a | |
| Axis of Parabola | Positive y-axis |
.png) |
Open Towards | Downward |
| Standard Equation | x2 = –4ay, a > 0 | |
| Coordinates of Focus | (0, –a) | |
| Coordinates of Vertex | (0, 0) | |
| Equation of Directrix | y = a | |
| Length of Latus Rectum | 4a | |
| Axis of Parabola | Negative y-axis |
❖ If the fixed point lies on the fixed line, then the set of points in the plane that are equidistant from the fixed point and the fixed line is a straight line through the fixed point and perpendicular to the fixed line.
We call this straight line the degenerate case of parabola.
❖ Ellipse
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
• The two fixed points are called the foci.
• The constant, which is the sum of the distances of a point on the ellipse from the two fixed points, is always greater than the distance between the two fixed points.
• The mid-point of the line segment joining the foci is called the centre of the ellipse.
• The line segment through the foci of the ellipse is called the major axis and the line segment through the centre and perpendicular to the major axis is called the minor axis.
• The end points of the major axis are called the vertices of the ellipse.
• The eccentricity of the ellipse is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.
• An ellipse is symmetric with respect to both the coordinate axes.
• The line segment that is perpendicular to the major axis of the ellipse through the focus and whose end points lie on the ellipse is called the latus rectum of the ellipse.
.png)
❖ Standard equations of ellipse
.png) |
Standard Equation | |
| Centre | (0, 0) | |
| Vertex | (±a, 0) | |
| End points of minor axis | (0, ±b) | |
| Foci | (±c, 0) | |
| Length of major axis | 2a along x-axis | |
| Length of minor Axis | 2b along y-axis | |
| Length between foci | 2c along x-axis | |
| Relation between a, b and c | a2 = b2 + c2 | |
| Length of latus rectum | ||
| Eccentricity (e < 1) |
.png) |
Standard Equation | |
| Centre | (0, 0) | |
| Vertex | (0, ±a) | |
| End points of minor axis | (±b, 0) | |
| Foci | (0, ±c) | |
| Length of major axis | 2a along y-axis | |
| Length of minor Axis | 2b along x-axis | |
| Length between foci | 2c along y-axis | |
| Relation between a, b and c | a2 = b2 + c2 | |
| Length of latus rectum | ||
| Eccentricity (e < 1) |
❖ Special cases of an ellipse
• When c = 0, i.e., both the foci merge together, then the ellipse becomes a circle.
• When c = a, then b = 0. In such a case, the ellipse reduces to a line segment joining the foci. This means the length of the line segment is 2c.
❖ Hyperbola
A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.
• The two fixed points are called the foci.
• The constant, which is the difference of the distances of a point on the hyperbola from the two fixed points, is always less than the distance between the two fixed points.
• The mid-point of the line segment joining the foci is called the centre of the hyperbola.
• The line through the foci is called the transverse axis and the line through the centre and perpendicular to the transverse axis is called the conjugate axis.
• The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola.
• The eccentricity of the hyperbola is the ratio of the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse.
• A hyperbola is symmetric with respect to both the coordinate axes.
• The line segment that is perpendicular to the transverse axis through the focus and whose end points lie on the hyperbola is called the latus rectum of the hyperbola.
❖ Standard equations of hyperbola
.png) |
Standard Equation | |
| Centre | (0, 0) | |
| Vertices | (±a, 0) | |
| Foci | (±c, 0) | |
| Conjugate axis | y-axis | |
| Transverse axis | x-axis | |
| Length of conjugate axis | 2b | |
| Length of transverse axis | 2a | |
| Length between foci | 2c | |
| Relation between a, b and c | c2 = a2 + b2 | |
| Length of latus rectum | 2b2 | |
| Eccentricity ( e > 1) |
.png) |
Standard Equation | |
| Centre | (0, 0) | |
| Vertices | (0, ±a) | |
| Foci | (0, ±c) | |
| Conjugate axis | x-axis | |
| Transverse axis | y-axis | |
| Length of conjugate axis | 2b | |
| Length of transverse axis | 2a | |
| Length between foci | 2c | |
| Relation between a, b and c | c2 = a2 + b2 | |
| Length of latus rectum | ||
| Eccentricity ( e > 1) |
❖ A hyperbola having equal lengths of both the axes, i.e., transverse and conjugate (a = b) is called an equilateral hyperbola.Chapter 12: Introduction to Three Dimensional Geometry
❖ Coordinate axes and coordinate planes
• In three-dimensions, the coordinate axes of a rectangular Cartesian coordinate system are three mutually perpendicular lines.
The axes are called x, y, and z-axes.
• The three planes determined by the pair of axes are the coordinate planes, called XY, YZ and ZX-planes.
The three coordinate planes divide the space into eight parts known as octants.
❖ Coordinates of a point
• In three-dimensional geometry, the coordinates of a point P are always written in the form of triplets i.e., (x, y, z).
Here, x, y, and z are the distances from the YZ, ZX and XY-planes.
Also, the coordinates of the origin are (0, 0, 0)
.png)
• The sign of the coordinates of a point determine the octant in which the point lies. The following table shows the signs of the coordinates in the eight octants.
| I | II | III | IV | V | VI | VII | VIII | |
| x | + | – | – | + | + | – | – | + |
| y | + | + | – | – | + | + | – | – |
| z | + | + | + | + | – | – | – | – |
• Coordinates of points lying on different axes
(i) Any point on the x-axis is of the form (x, 0, 0)
(ii) Any point on the y-axis is of the form (0, y, 0)
(iii) Any point on the z-axis is of the form (0, 0, z)
• Coordinates of points lying in different planes
(i) Coordinates of a point in the YZ-plane are of the form (0, y, z)
(ii) Coordinates of a point in the XY-plane are of the form (x, y, 0)
(iii) Coordinates of a point in the ZX-plane are of the form (x, 0, z)
❖ Distance between two points is given by
This is known as the distance formula.
❖ Section formula
The coordinates of point R, which divides the line segment joining two points

• internally in the ratio m: n are
• externally in the ratio m: n are
❖ The coordinates of the mid-point of the line joining the points are .
❖ The coordinates of the centroid of a triangle whose vertices are and x3, y3, z3 areChapter 14: Mathematical Reasoning
❖ A sentence is called a mathematically acceptable statement if it is either true or false, but not both. Statements are denoted by small letters p, q, r, s, etc.
Example: Consider the following sentences:
• “The value of iota is –1.”
It is a statement. Since we know that , the given sentence is false.
• “The number 0 is the smallest whole number.”
It is a statement as this sentence is always true.
• “Do you have internet at your home?”
It is not a statement as it is a question.
❖ Remember
• Sentences involving variable time such as today, tomorrow and yesterday are not statements.
• Sentences involving an exclamation, a question or an order are not statements.
• Sentences involving pronouns such as he or she, unless a particular person is referred to, are not statements.
• Sentences involving pronouns for variable places such as here and there are not statements.
❖ The denial of a statement is called the negation of the statement.
• If p is a statement, then the negation of p is also a statement, and is denoted by ~p, and is read as “not p”.
• While writing the negation of a statement, phrases such as “It is not the case” or “It is false that” are used.
Example:
Write the negation of the following statement:
p: The square root of every positive number is positive.
Solution:
The negation of the given statement can be written as:
The square root of every positive number is not positive.
Or
It is false that the square root of every positive number is positive.
Or
It is not the case that the square root of every positive number is positive.
Or
There exists a positive number whose square root is not positive.
❖ A compound statement is one that is made up of two or more statements.
• Each smaller statement is called the component of the compound statement.
• These components are joined by words such as “And” and “Or”. These are called connectors or connecting words.
Example:
The statement “27 is a multiple of 9 and it is even” is a compound statement.
Its component statements are:
p: “27 is a multiple of 9.”
q: “27 is even.”
Here, the connecting word is “And”.
• A statement with “And” is not always a compound statement.
Example: Water can be prepared by the mixture of hydrogen and oxygen in a certain ratio.
This statement is not a compound statement.
❖ Rules regarding the connector “And”
• The compound statement with the connector “And” is true if all its component statements are true.
• The compound statement with the connector “And” is false if any/both of its component statements is/are false.
❖ Rules regarding the connector “Or”
• A compound statement with the connector “Or” is true when one component statement is true, or both the component statements are true.
• A compound statement with the connector “Or” is false when both the component statements are false.
❖ Types of “Or”
• Exclusive “Or”: A compound statement with the connector “Or” in which either of the component statements may be true, but not both
Example: A student can take home science or painting as his/her additional subject in class XI.
• Inclusive “Or”: A compound statement with the connector “Or” in which either of the component statements or both may be true.
Example: In an equilateral triangle, all the three sides are of equal length or all the three angles are of equal measure.
❖ Some statements may contain special phrases such as “There exists”, “For all”, “For every”. These are called quantifiers.
❖ Implication statement “if-then”: The sentence “if p, then q” says that in the event if p is true, then q must be true. It does not say anything for q when p is false.
• A sentence “if p, then q” can be written in the following ways:
(i) p implies q (denoted by p
(ii) p is a sufficient condition for q
(iii) p only if q
(iv) q is a necessary condition for p
(v) ~q implies ~p
❖ Contrapositive and converse of a statement
• The contrapositive of the statement p
• The converse of a statement p
Example: Write the converse and the contrapositive of the following statement:
“If an object is made up of only line segments, then it is a polygon.”
Solution:
The converse of the given statement can be written as follows:
“If an object is a polygon, then it is made up of only line segments.”
The contrapositive of the given statement can be written as follows:
“If an object is not a polygon, then it is not made up of only line segments.”
❖ The equivalent forms of the statement “p if and only if q” (denoted by p
• q if and only if p
• p if and only if q
• p is a necessary and sufficient condition for q and vice-versa
❖ Validating statements
• In order to show that the statement “p and q” is true, the following steps are followed:
1. Show that statement p is true.
2. Show that statement q is true.
• In order to show that the statement “p or q is true”, the following cases are to be considered.
1. Assuming that p is false, show that q must be true.
2. Assuming that q is false, show that p must be true.
• In order to prove the statement “if p, then q’, we need to show that any one of the following cases is true.
1. Assuming that p is true, prove that q must be true. (Direct method)
2. Assuming that q is false, prove that p must be false. (Contrapositive method)
• In order to prove the statement “p if and only if q”, we need to follow the following steps:
1. If p is true, then q is true.
2. If q is true, then p is true.
• Method of contradiction
To check whether a statement p is true, we assume that p is not true, i.e., ~p is true, and then we arrive at some result which contradicts our assumption. Therefore, we conclude that p is true.
This method of proving a given statement to be true is called the contradiction method.
• Using a counter example
In order to disprove a statement, we give an example of the situation where the statement is not valid. Such an example is called a counter example.
In mathematics, counter examples are used for disproving a statement. However, generating examples in favour of a statement does not provide validity to the statement.
Example: The statement “, is true for n = 1, 2, but it is not true for n = 3, 4.
Here, n = 3 and 4 are the counter examples of the given statement. Since the statement is not true for each n ∈ N, the given statement is false. Chapter 15: Statistics
❖ The measures of central tendency, mean, median and mode give us a rough idea where data points are centered.
❖ The dispersion or scatter in a data is measured on the basis of observations and the types of measure of central tendency used. The measures of dispersion are as follows:
• Range
• Quartile deviation
• Mean deviation
• Standard deviation
❖ Range of a series = Maximum value – Minimum value
❖ Mean deviation about mean
• For ungrouped data: , is the mean given by
• For grouped data: , is the mean given by
❖ Mean deviation about median [M.D.(M)]
• For ungrouped data: is the median
• For grouped data: where M is the median and
❖ The mean of the squares of the deviations from mean is called the variance and it is denoted by
❖ Variance of data
• For ungrouped data: (In direct method) or (In shortcut method), where is the mean.
• For discrete frequency distribution: (In direct method) or (In shortcut method), where
 is the mean and.
is the mean and.• For continuous frequency distribution: or (In direct method) or (In shortcut method), where
xi = class marks of the class intervals,
 = mean,
= mean,  , h = width of the class intervals, , where A is the assumed mean.
, h = width of the class intervals, , where A is the assumed mean.❖ Adding (or subtracting) a positive number to (or from) each observation does not affect the variance.
❖ If each observation is multiplied with a constant k, then the variance of the resulting observations becomes k2 times the original variance.
❖ Standard deviation is the square root of variance and it is denoted by
❖ Coefficient of variation
The measure of variability, which is independent of units, is called the coefficient of variation. The coefficient of variation (C.V.) is defined as
Where,
• For comparing the variability or dispersion of two series, we first calculate the C.Vs of each series.
The series having higher C.V. is said to be more variable than the other and the series having lower C.V. is said to be more consistent than the other.
• For two series with equal mean values, the series with greater standard deviation (or variance) is more variable or dispersed than the other.
Also, the series with lower value of standard deviation (or variance) is said to be more consistent or less scattered than the other.Chapter 16: Probability
❖ An experiment is called a random experiment if it satisfies the following two conditions:
• It has more than one possible outcome
• It is not possible to predict the outcome in advance
❖ A possible result of a random experiment is called its outcome.
❖ The set of all possible outcomes of a random experiment is called the sample space associated with the experiment. It is denoted by S.
Each element of the sample space i.e., each outcome of the random experiment is called the sample point.
❖ Any subset (E) of a sample space is called an event.
• The event (E) of a sample space (S) is said to have occurred if the outcome (
• If the outcome (
❖ Types of events
• Impossible event: An empty set (ϕ) is called an impossible event.
• Sure event: The whole sample space (S) is called a sure event.
• Simple event: If an event (E) has only one sample point of a sample space, then it is called a simple (or elementary) event.
In a sample space containing n distinct elements, there are exactly n simple events.
• Compound event: If an event has more than one sample point, it is called a compound event.
Example: Consider an experiment of selecting numbers from first 50 natural numbers, then the sample space (S) is given as
S = {1, 2, 3, 4, … 49, 50}
In this case,
(i) The event “Getting a number that is a multiple of both 7 and 9” is an impossible event as there is no outcome related to it.
(ii) The event “Getting a perfect square that is more than 40” is a simple event since E = {49}.
(iii) The event “Getting an odd multiple of 13” is a compound event since E = {13, 39}.
❖ Algebra of events
• Complementary event: For every event A, there corresponds another event Aʹ called the complementary event to A. It is also called the event ‘not A’.
Aʹ = {
• Event ‘A or B’: When sets A and B are two events associated with a sample space, then the set A ⋃ B is the event ‘either A or B or both’.
That is, event ‘A or B’ = A ⋃ B = {
• Event ‘A and B’: When sets A and B are two events associated with a sample space, then the set A ⋂ B is the event ‘A and B’.
That is, event ‘A and B’ = A ⋂ B = {
• Event ‘A but not B’: When sets A and B are two events associated with a sample space, then the set A – B is the event ‘A but not B’.
That is, event ‘A but not B’ = A – B = A ⋂ Bʹ = {
Example:
Consider the experiment of tossing 2 coins. Let A be the event ‘getting at least one head’ and B be the event ‘getting exactly two heads’. Find the sets representing the events
(i) complement of ‘A or B’
(ii) A and B
(iii) A but not B
Solution:
Here, S = {HH, HT, TH, TT}
A = {HH, HT, TH}, B = {HH}
(i) A or B = A ⋃ B = {HH, HT, TH}
Hence, complement of ‘A or B’ = (A or B)ʹ = (A ⋃ B)ʹ = {TT}
(ii) A and B = A ⋂ B = {HH}
(iii) A but not B = A – B = {HT, TH}
❖ Two events, A and B, are called mutually exclusive events if the occurrence of any one of them excludes the occurrence of the other event i.e., if they cannot occur simultaneously.
In this case, sets A and B are disjoint i.e., A ⋂ B = ϕ
❖ If E1, E2, … En are n events of a sample space S, and if
E1 ⋃ E2 ⋃ …. ⋃ En = , then
E1, E2 … En are called mutually exhaustive events.
In other words, at least one of E1, E2 … En necessarily occurs whenever the experiment is performed.
❖ The events E1, E2, … En, i.e., n events of a sample space (S) are called mutually exclusive and exhaustive events if
• Ei ⋂ Ej = ϕ for i ≠ j i.e., events Ei and Ej are pairwise disjoint, and
•
❖ The number P (
• 0 ≤ P(
• ΣP(
• For any event A, P(A) = ΣP(
❖ For a finite sample space, S, with equally likely outcomes, the probability of an event A is denoted as P (A) and it is given by
,
Where, n(A) = Number of elements in set A and n(S) = Number of elements in set S
❖ If A and B are two events, then P (A ⋃ B) = P (A) + P (B) – P (A ⋂ B)
❖ If A and B are mutually exclusive events, then P (A ⋃ B) = P (A) + P (B)
❖ If A is any event, then P (A′) = 1 – P (A)Chapter 13: Limits and Derivatives
❖ Limit of a function
• is the expected value of f at x = a, given the values of f near x to the left of a. This value is called the left hand limit of f(x) at a.
• is the expected value of f at x = a, given the values of f near x to the right of a. This value is called the right hand limit of f(x) at a.
• If the right and left hand limits coincide, we call that common value the limit of f(x) at x = a, and denote it by .
• For a function f and a real number a, and f(a) may not be the same.
❖ Algebra of limits
Let f and g be two functions such that both exist. Then,
•
•
• , where
•
❖ Some standard limits
• For a polynomial function f(x), .
• If f(x) is a rational function of the form , where g(x) and h(x) are polynomial functions, such that h(x) ≠ 0, then .
• , where n is a positive integer or any rational number and a is positive
•
•
❖ Let f and g be two real-valued functions with the same domain, such that f(x) ≤ g(x) for all x in the domain of definition.
For some a, if both exist, then .
❖ Sandwich theorem
Let f, g, and h be real functions such that f(x) ≤ g(x) ≤ h(x) for all x in the common domain of definition. For some real number a, if .
❖ Derivatives
• Suppose f is a real-valued function and a is a point in its domain of definition. The derivative of f at a [denoted by f′(a)] is defined as
, provided the limit exists.
Derivative of f(x) at a is denoted by f′(a).
• Suppose f is a real-valued function. The derivative of f {denoted by f'(x) or} is defined as
, provided the limit exists.
This definition of derivative is called the first principle of derivative.
❖ Algebra of derivatives of functions
For the functions u and v (provided uʹ and vʹ are defined in a common domain),
•
•
•
❖ Some standard derivatives
• for any positive integer n
•
•
•
•
