Chapter 1: Integers
❖ Integers are the collection of whole numbers and negative numbers i.e., –4, –2, 0, 1, 2, etc. are all integers.
❖ On a number line,
   • to add a positive integer, move as many units to the right as the given integer and to add a negative integer, move to the left
   • to subtract a positive integer, move as many units to the left as the given integer and to subtract a negative integer, move to the right

❖ Properties of addition and subtraction of integers
   • Integers are closed under addition and subtraction.
     For two integers, a and b, a + b and a – b are integers.
   • Addition is commutative for integers.
     For integers, a and b, a + b = b + a
   • Subtraction is not commutative for integers.                                          
     For integers, a and b, a – b ≠ b – a
   • Addition is associative for integers. For integers, a, b, and c:
     a + (b + c) = (a + b) + c
   • Subtraction is not associative for integers.
   • When 0 is added to any integer, say a, the same integer is obtained. Therefore, 0 is the additive identity of integers.
     a + 0 = a = 0 + a

❖ Multiplication of integers
  • To multiply a positive integer and a negative integer, the numbers are multiplied as whole numbers and a negative sign (–) is put before the product.
  • If the number of negative integers in a product is even, then the product is a positive integer. If the number of negative integers in a product is odd, then the   product is a negative integer.

❖ Properties of multiplication of integers
  • Integers are closed under multiplication. For integers, a and b, a × b is an integer.
  • Integers are commutative under multiplication.
    For integers, a and b, a × b = b × a
  • The product of an integer and zero is zero.
  • When an integer is multiplied by 1, it gives the same integer.
    1 × a = a × 1 = a
    Therefore, 1 is the multiplicative identity for integers.
  • Integers are associative under multiplication.   
    For integers, a, b and c: a × (b × c) = (a × b) × c
  • Multiplication is distributive over addition and subtraction for integers. For integers, a, b, and c: 
    a × (b + c) = a × b + a × c
    a × (b – c) = a × b – a × c
  • These properties can be used to simplify calculations.
     For example: 17 × 49 = 17 × (50 – 1) = 850 – 17 = 833

❖ Division of integers
  • To divide a positive integer by a negative integer, the division is carried out as in whole numbers and then a negative sign (–) is put before the quotient.

    For two positive integers, a and b, $\left(a\right)÷(-b)=\left(\frac{a}{b}\right)$.
  • When a negative integer is divided by another negative integer, a positive quotient is obtained.
    For two positive integers, a and b, $(-a)÷(-b)=\frac{a}{b}$
  • For any integer a, a ÷ 0 is not defined and a ÷ 1 = aChapter 2: Fractions and Decimals
 
❖ The fractions in which the numerator is smaller than the denominator are called proper fractions. For example, $\frac{2}{3},\frac{5}{7},\frac{13}{17}, \mathrm{etc}.$
❖ If the numerator of a fraction is bigger than its denominator, then it is an improper fraction. For example, $\frac{9}{4},\frac{8}{5},\frac{11}{6}, \mathrm{etc}$
❖ A mixed fraction has a whole part and a fractional part. For e.g., $2\frac{4}{7},3\frac{9}{8}, \mathrm{etc}$.
❖ Multiplication of fractions
• Multiplication of  a whole number with a fraction
A whole number is multiplied with a proper or improper fraction by multiplying the whole number with the numerator of the fraction, keeping the denominator constant.
• Multiplication of a whole number with a mixed fraction
A mixed fraction is first converted into an improper fraction and then multiplied with the whole number.
• Multiplication of two fractions
When two fractions are multiplied, the product is obtained as.
 $\frac{\mathrm{Product} \mathrm{of} \mathrm{numerators}}{\mathrm{Product} \mathrm{of} \mathrm{denominators}}$
 
❖ Relation between fractions and their product
The product of two proper fractions is always less than each of the fractions.
The product of two improper fractions is greater than each of the fractions.
The product of a proper fraction and an improper fraction is greater than the proper fraction, but less than the improper fraction.
 
❖ Division of fractions
• Two non-zero numbers whose product is 1 are the reciprocals of each other.
• To divide a whole number or a fraction by a fraction, the whole number or the fraction is multiplied with the reciprocal of the divisor.
 
❖ Multiplication of decimals
• To multiply two decimal numbers, the numbers have to be first multiplied as whole numbers. Then, decimal is put in the product by counting the digits from the rightmost digit equal to the sum  of the number of digits to the right of the decimal in both the numbers.
For example,
0.32 × 0.4
Here, the number of digits to the right of the decimal in 0.32 is 2 and in 0.4 is 1.
32 × 4 = 128
Putting the decimal in 128 by counting (2 + 1) = 3 places to the left of 8, we obtain:
0.32 × 0.4 = 0.128
• When a decimal number is multiplied by 10, 100, or 1000, we obtain the product as in the decimal number, but the decimal in the product is shifted to the right to as many places as there are zeroes.
For Example: 0.42 × 1000 = 420
 
❖ Division of decimal numbers
•  To divide a decimal number by a whole number, it is first divided as whole numbers and then the decimal is put in the quotient to as many places from the right as in the decimal number.
For example, $\frac{8.4}{7}=1.2$
• When a decimal number is divided by 10, 100, or 1000, the quotient is same as the decimal number, but the decimal point in the quotient shifts to the left by as many places as there are zeroes.
For Example: $\frac{43.2}{1000}=0.0432$
• When a decimal number is divided by another decimal number, then the division is carried out taking the numbers as whole numbers and the decimal is put in the quotient at as many places from the rightmost digit as the difference between the number of digits to the right of the decimal in the numerator and the denominator.
For example,
$\frac{0.96}{1.2}$
Here, numerator has two digits to the right of the decimal and denominator has 1 digit.
$\frac{96}{12}=8$
Putting the decimal (2 – 1) = 1 place to the left of 8, we obtain:
$\frac{0.96}{1.2}=0.8$Chapter 3: Data Handling
❖ There are various ways of collecting data. Before collecting data, one should know the purpose for which it would be used.

❖ Mean
• Mean or average of a data is given by the sum of all observations divided by the number of observations, that is,
  $\mathrm{Mean} = \frac{\mathrm{Sum} \mathrm{of} \mathrm{observations}}{\mathrm{Number} \mathrm{of} \mathrm{observations}}$
• Mean always lies between the highest and lowest observations of the data.
• It is not necessary that mean is any one of the observations of the data.

❖ Range is the difference between the highest and lowest observations of the data.

❖ Mode
• The mode of a set of observations is the observation that occurs most often.
• Mode of a large data can be calculated by forming a tally marks table.

❖ Median
• The median of a data is the value of the middle observation, when the data is arranged in ascending or descending order.
• The median divides the data into two equal halves.

❖ Mean, median, and mode are measures of central tendency.

❖Bar graphs
• Bar graph is another way of representing the data using bars of uniform widths. The lengths of the bars depend upon the frequency and scale chosen.
• Double bar graphs are also drawn as bar graphs. It is the collection of two sets of data on the same graph. It is helpful in comparing the two sets of data.

❖ Probability implies the certainty of the happening of an event.

Example: 
A bag contains one green, one red, one blue, and one black ball. What is the probability that the ball drawn is red?

Solution:
When a ball is drawn, it can be any of the four balls.
  Probability of drawing a red ball $=\frac{1}{4}$Chapter 4: Simple Equations
 
❖ A variable can take different numerical values. Its value is not fixed. It is denoted by alphabets, a, b, c, x, y, z, etc.

❖ An equation is a condition on a variable such that both sides of the equation have equal values. For example, 4x – 9 =3, 2x + 4 = 13 – x, etc.
   The expression on the left is known as left hand side (LHS) and on the right as right hand side (RHS).

❖ An equation is used in finding the missing value in a statement.
 
Example: The difference between two integers is 5 and the greater integer is 7. Find the other integer.
Solution: Let the other number be x.
7 – x = 5
❖ An equation remains unchanged if
• the expressions on both its sides are interchanged
• the same number is added or subtracted on both sides of the equation
• a non-zero number is multiplied or divided on both sides of the equation

❖ The value of variable that satisfies the equation is known as its solution.

❖ Solving an equation by performing same mathematical operation on both sides.
Example: 3x – 7 = 2
3x – 7 + 7 = 2 + 7
3x = 9
$\frac{3x}{3}=\frac{9}{3}$
 x = 3
Therefore, x = 3 is the solution of 3x – 7 = 2

❖ Solving an equation by transposing
If a number is transposed from one side of an equation to the other, then its sign is changed.
 
Example: x – 7 = 5
x = 5 + 7  (Transposing –7) Chapter 5: Lines and Angles
 
❖ An angle is made when two lines or line segments meet.
 When the sum of the measures of two angles is 90°, the angles are called complementary angles. For example: 75° and 15°

❖ When the sum of the measures of two angles is 180°, the angles are called supplementary angles. For example: 110° and 70°

❖ A pair of angles are called adjacent angles, if
• they have a common vertex
• they have a common arm
• the non-common arms are on either side of the common arm
In the following figure, ∠AOB and ∠BOC are adjacent angles.

 ❖ A linear pair is a pair of adjacent angles whose non-common sides are opposite rays i.e., the sum of the measures of the adjacent angles is 180°.
In the following figure,  ∠AOC and  ∠BOC form a linear pair.

❖ When two lines meet, the common meeting point is known as the point of intersection.
In the following figure, O is the point of intersection of lines l and m.
 
 
❖ When two lines intersect, the vertically opposite angles so formed are equal.
In the following figure,  ∠AOC =  ∠BOD and  ∠AOD =  ∠BOC.

 
❖ When two lines never meet i.e., the distance between them always remain equal, the lines are called parallel lines.
In the following figure, lines p and q are parallel.
 
❖ A transversal is a line intersecting a pair of lines.

Here, line l is a transversal with respect to lines p and q.
• ∠1 and  ∠5,  ∠2 and  ∠6,  ∠3 and  ∠7,  ∠4 and  ∠8 are pairs of corresponding angles.
• ∠3 and  ∠5,  ∠4 and  ∠6 are pairs of alternate interior angles.
• ∠1 and  ∠7,  ∠2 and  ∠8 are pairs of alternate exterior angles.
• ∠3 and  ∠6,  ∠4 and  ∠5 are pairs of interior angles on the same side of the transversal.
 
❖ If lines p and q are parallel, then the

• corresponding angles are equal i.e., ∠1 =  ∠5,  ∠2 =  ∠6,  ∠3 =  ∠7,  ∠4 =  ∠8
• alternative angles are equal i.e., ∠3 =  ∠5,  ∠4 =  ∠6,  ∠1 =  ∠7,  ∠2 =  ∠8
• pair of interior angles on the same side of the transversal are supplementary i.e., ∠3 + ∠6 = 180°, ∠5 + ∠4 = 180°
 
❖ If a pair of lines is cut by a transversal and if the pairs of corresponding angles are equal, then the lines are parallel.
 
❖ If a pair of lines is cut by a transversal and if the pairs of alternate angles are equal, then the lines are parallel.
 
❖ If a pair of lines is cut by a transversal and if the sum of the interior angles on the same side of the transversal is supplementary, then the lines are parallel.Chapter 6: The Triangle and its Properties
 
❖ A triangle is a simple closed curve made up of three line segments.
     It has three vertices, three sides and three angles.

❖ Triangles can be classified on the basis of their sides as:
• Scalene – All the three sides of the triangle are
• Isosceles – Exactly two sides of the triangle are equal
• Equilateral – All the sides of the triangle are equal

❖ On the basis of angles, triangles can be classified as:
• Acute-angled – All the angles of the triangle are less than 90°
• Obtuse-angled – Any one of the angles of the triangle is greater than 90°
• Right-angled – Any one of the angles of the triangle is 90°

❖ Median of a triangle
A median is a line segment joining the vertex of a triangle to the mid-point of the opposite side.
• In the given ΔABC, if AD = DC, then BD is the median of ΔABC with respect to the side AC.


 • A triangle has three medians, one for each side.

❖ Altitude of a triangle
An altitude is the perpendicular drawn from the vertex of a triangle to its opposite side.
• In the following figure, AD is the altitude of ΔABC with respect to side BC.

• A triangle has three altitudes, one from each vertex.
• The altitude of a triangle may or may not lie inside the triangle.
  For example, for ΔPQR, its altitude PS lies outside it.


❖ Exterior-angle property of triangles
In a triangle, the measure of an exterior angle is equal to the sum of the measures of its opposite interior angles.
 
In the given ΔABC,  ∠ACD is an exterior angle of ΔABC.
∠ACD =  ∠A +  ∠B

 
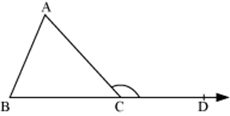
❖ Angle-sum property of triangles
The sum of the measures of all the interior angles of a triangle is 180°.

❖ Equilateral triangle
• All the sides of an equilateral triangle are equal.
• Each angle is of measure 60°.

❖ Isosceles triangle
• Two sides are of equal length.
• Angles opposite to equal sides are equal.

❖ Triangle inequality: In a triangle, the sum of the lengths of any two sides is greater than the length of the third side. Also, the difference between the lengths of any two sides of a triangle is less than the length of the third side.

❖ Right-angled triangle
• A triangle with one of the angles as 90°, is called a right-angled triangle.
In the following figure, ΔABC is a right-angled triangle with  ∠B = 90°
 

• The side opposite to the right angle is called its hypotenuse. The other two sides are called the legs of the right-angled triangle, i.e., in the given figure, AC is the hypotenuse and AB, BC are the legs.

❖ Pythagoras Theorem and its converse
• In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides i.e., AC² = AB² + BC².
This property is called Pythagoras Theorem.
• If Pythagoras Theorem holds in a triangle, then it is a right-angled triangle. This is the converse of Pythagoras Theorem.
 
Example:

Here, BC² = AB² + AC²
Therefore, Pythagoras Theorem holds in ΔABC. Thus, it is a right-angled triangle at  ∠A.Chapter 7: Congruence of Triangles
 
❖ Two objects are said to be congruent, if they are exact copies of each other.

❖ Two lines segments are congruent, if they are equal in length.

❖ Two angles are congruent, if they have the same measure.

❖ Congruence of triangles
In congruence of triangles, not only sides and angles are taken into account but also the correspondence of vertices is important. For example, if ΔABC is congruent to ΔPQR, then it may or may not be congruent to ΔQPR or ΔPRQ.

❖ SSS congruence criterion
If three sides of a triangle are equal to the three corresponding sides of another triangle, then the triangles are congruent.

❖ SAS congruence criterion
If two sides of a triangle and the angle included between them are equal to the corresponding two sides and included angle of another triangle, then the triangles are congruent.

❖ ASA congruence criterion
If two angles and included side of a triangle are equal to the two corresponding angles and the included side of another triangle, then the triangles are congruent.

❖ RHS congruence criterion
If the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one side of another right-angled triangle, then the triangles are congruent.Chapter 8: Comparing Quantities
 
❖ Two quantities can be compared, if their units are the same.
❖ Two ratios are said to be equivalent, if their corresponding fractions are equal.
❖ Two ratios a: b and c: d are said to be in proportion, if 25 $\frac{a}{b}=\frac{c}{d}$.

❖ Percentage
• Percentages are another way of comparing quantities. Percentages are numerators of fractions with denominator 100. It is represented by the symbol % and means hundredths too, i.e., 25% $\frac{25}{100}=0.25$
 
Example: In a bag there are 6 blue marbles, 4 red marbles and 5 green marbles. What percent of total marbles are blue?

Solution: Total number of marbles = 6 + 4 + 5 = 15
Number of blue marbles = 6
Percentage of blue marbles $\frac{6}{15}\times 10=40\%$
• Fractional numbers can be converted into percentages by multiplying them by 100%.
  (i) Percentages related to proper fractions are less than 100.
  (ii) Percentages related to improper fractions are more than 100.
• Decimals can be converted into percents by multiplying them by 100%.
• Percentages can be converted into fractions or decimals by dividing them by 100.
• When added, all parts of a whole give whole or 100%.
• If we know the percentage of something, then we can find its quantity in the whole (if the quantity of the whole is known).
Example: In a particular month, Ravi saves 28% of his income. If his monthly salary is Rs 5000, then how much amount of money did he spend in that month?

Solution: Income = Savings + Expenditure
Percentage of income that Ravi spent = (100 – 28)% = 72%
Amount of money Ravi spent = 72% of Rs 5000
$$\begin{gathered} =\frac{72}{100}\times 5000 \\ = \mathrm{Rs} 3600 \end{gathered}$$
❖ Increase or decrease in a quantity as a percentage is given by $\frac{\mathrm{Amount} \mathrm{of} \mathrm{change}}{\mathrm{Original} \mathrm{amount}}\times 100$
❖ Profit and loss
• The buying price of an article is called its cost price (CP).
• The price at which the article is sold is its selling price (SP).
•  (i) If CP < SP, then profit is made and Profit = SP – CP
   (ii) If CP = SP, then there is a no profit, no loss situation.
   (iii) If CP > SP, then loss is incurred and Loss = CP – SP
• Profit or loss can be converted into percentage as:
 $$\begin{gathered} \left(\mathrm{i}\right) \mathrm{Profit} \% = \frac{\mathrm{Profit}}{\mathrm{CP}}\times 100 \\ \left(\mathrm{ii}\right) \mathrm{Loss} \% = \frac{\mathrm{Loss}}{\mathrm{CP}} \times 100 \end{gathered}$$

❖ Simple interest
• The amount of money that is borrowed is known as principal and is denoted by P.
• The extra amount of money that one has to pay is known as interest and is denoted by I.
• The total amount of money A that one pays back is equal to the sum of principal and interest.
• The simple interest (S.I.) on the principal (P) when borrowed for T years at R% rate of interest per year is given by the formula $\mathrm{S}.\mathrm{I}.=\frac{P\times R\times T}{100}$Chapter 9: Rational Numbers
❖ The numbers, which can be written in the form$\frac{p}{q}$, where p and q are integers and q  0, are called rational numbers. Rational numbers can be positive as well as negative.
For example,$-\frac{2}{7},\frac{41}{366},2=\frac{2}{1}$ etc.

❖ Equivalent rational numbers can be obtained by multiplying or dividing the numerator and denominator of a rational number by the same non-zero integer.

❖ Rational numbers on number line
• Rational numbers can be represented on number line as fractions and integers are represented.
• Negative rational numbers are marked to the left of 0 while positive rational numbers are marked to the right of 0.
Example: Represent $-\frac{2}{5}$ on the number line.
Solution:
The given rational number is negative. Therefore, it will lie to the left of 0.
The space between –1 and 0 is divided into 5 equal parts. Therefore, each part represents $-\frac{1}{5}$. On marking  at 2 units to the left of 0, we obtain the number line as follows:
 
❖ Standard form of rational numbers
• A rational number is said to be in the standard form if its numerator and denominator have no common factor other than 1.
• Rational numbers can be reduced to the standard form by dividing their numerator and denominator by their HCF.

❖ Comparing rational numbers
• Two positive rational numbers can be compared as in fractions.
• Two negative rational numbers can be compared by ignoring their negative signs and then reversing their order.

❖ Rational numbers between two rational numbers can be found by first converting them to rational numbers with same denominator.
Example: Find 4 rational numbers between$-\frac{2}{3}\mathrm{and} -\frac{1}{5}$.
Solution:
 $$\begin{gathered} -\frac{2}{3}\times \frac{5}{5}=-\frac{10}{15} \\ -\frac{1}{5}\times \frac{3}{3}=-\frac{3}{15} \\ \therefore -\frac{10}{15}<-\frac{9}{15}<-\frac{8}{15}<-\frac{7}{15}<-\frac{6}{15}<-\frac{3}{15} \end{gathered}$$
 
❖ There are unlimited rational numbers between two rational numbers.

❖ All the operations on rational numbers are performed as in fractions.

❖ When 0 is added to any rational number, say$\frac{p}{q}$, the same rational number is obtained. Therefore, 0 is the additive identity of rational numbers.
$\frac{p}{q}+0=\frac{p}{q}=0+\frac{p}{q}$

❖ Addition of rational numbers
Rational numbers with the same denominator can be added by adding the numerators while keeping the denominators constant.
For any non-zero rational numbers $\frac{a}{b}\mathrm{and} \frac{\mathit{c}}{\mathit{b}}$, $\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}$.
❖ Additive inverse of rational numbers
For any non-zero rational number $\frac{a}{b}$, there exists a unique rational number $-\frac{a}{b}$ such that $\frac{a}{b}+\left(-\frac{a}{b}\right)=0. \frac{a}{b} \mathrm{and} \frac{a}{b}$are the additive inverses of each other.
 Subtraction of rational numbers
Rational numbers can be subtracted by adding the additive inverse of the rational number that is being subtracted to the other rational number. For any non-zero rational numbers $\frac{a}{b}\mathrm{and} \frac{c}{d},\frac{a}{b} -\frac{c}{d}=\frac{a}{b} +\left(-\frac{c}{d}\right).$
❖ Multiplication of rational numbers
Rational numbers can be multiplied by multiplying their numerators with numerators and denominators with the denominators. For any non-zero rational numbers
$\frac{a}{b}\mathrm{and}\frac{c}{d}, \frac{\mathit{a}}{\mathit{b}}\times \frac{\mathit{c}}{\mathit{d}}\mathit{=}\frac{\mathit{a}\mathit{\times }\mathit{c}}{\mathit{b}\mathit{\times }\mathit{d}}$ .

❖ Division of rational numbers
Rational numbers can be divided by multiplying one rational number with the reciprocal of the other.
For any non-zero rational numbers $\frac{a}{b}\mathrm{and} \frac{c}{d},\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}\times \frac{d}{c}$.

Chapter 10: Practical Geometry
 
❖ A line parallel to a given line, through a point not on the line, can be constructed by using the properties of transversal and parallel lines.
    Example: Draw a line parallel to a given line m, through a point P, outside the line m.
 

Solution:
Steps of construction:
(1) Take any point Q on m and join PQ.
(2) With Q as centre and convenient radius, draw an arc cutting m at R and PQ at S.
(3) With P as centre and the same radius, draw an arc TU cutting PQ at V; then V as centre and radius equal to RS, draw an arc cutting TU at X.
(4) Join PX to draw a line n.
 
 Now, the line n is parallel to m.  
 
❖ Construction of a triangle
A triangle can be constructed if
• All its three sides are known (SSS criterion)
• Two sides and the angle between them are known (SAS criterion)
• Two angles and the side between them are known (ASA criterion)
• Hypotenuse and a leg are known, if the triangle is right-angled (RHS criterion)

Example 1: Construct a triangle whose sides are 2 cm, 4 cm and 7 cm.

Solution:
(1) Draw a line segment AB of length 7 cm. With A as centre and radius equal to 2 cm, draw an arc.
(2) With B as centre and radius 4 cm, draw another arc cutting the earlier drawn arc at C.            
(3) Join AC and BC to get ΔABC.
  

Example 2: Construct ΔABC where BC = 7 cm, AB = 5 cm and  ∠ABC = 30°

Solution:
(1) Draw a line segment BC of length 7 cm and at B draw a ray BX, making an angle of 30° with BC.
(2) With B as centre and radius equal to 5 cm, draw an arc cutting BX at A.                    
(3) Join AC to get the required ΔABC.
 
 
Example 3: Construct ΔPQR, where  ∠PQR = 60°,  ∠PRQ = 45° and QR = 4 cm.

Solution:
(1) Draw a line segment QR of length 4 cm and draw a ray QX, making an angle of 60° with QR       
(2) Now, draw ray RY, making angle of 45° with QR and intersecting QX at P. The resulting ΔPQR is the required triangle.

 ⊥
Example 4: Construct ΔXYZ, right-angled at Y, with XZ = 5 cm and YZ = 3 cm.

Solution:
(1) Draw a line segment YZ of length 3 cm. At Y, draw MY⊥YZ.            
(2) With Z as centre and radius equal to 5 cm, draw an arc intersection MY at X. Join XZ to get the required ΔXYZ.
 

Chapter 11: Perimeter and Area
 
❖ Perimeter is the distance around a closed figure.
• Perimeter of a square = 4 × (Side)
• Perimeter of a rectangle = 2 (Length + Breadth)
• Area is the region enclosed by a closed figure.
• Area of a square = (Side)²
• Area of a rectangle = (Length × Breadth)

❖ Area of a parallelogram
• The perpendicular dropped on a side from its opposite vertex is known as the height and the side is known as the base.
• Area of a parallelogram = Base × Height


❖ Area of a triangle
• Area of a triangle $=\frac{1}{2}\times \mathrm{Base} \times \mathrm{Height}$
• All the congruent triangles are equal in area, but the triangles having equal areas may or may not be congruent.

❖ Circumference and area of a circle
• The distance around a circular region is known as its circumference.
  Circumference of a circle = π × Diameter = 2π × Radius
• The value of pi (π) is $\frac{22}{7}$or 3.14
• Area of a circle = π × (Radius)²
❖ Conversion of units of area
• 1 cm² = 100 mm²
• 1 m² = 100 cm × 100 cm = 10000 cm²
• 1 hectare = 10000 m²Chapter 12: Algebraic Expressions
 
❖ Algebraic expressions are formed by combining variables with constants using operations of addition, subtraction, multiplication and division.
   For example: 4xy, 2x² – 3, 7xy + 2x, etc.
• In an algebraic expression, say 2xy – 3x² + 2; 2xy, (–3x²), 2 are known as the terms of the expression.
• The expression 2xy – 3x² +2 is formed by adding the terms 2xy, (–3x²) and 2 where 2, x, y are factors of the term 2xy; (–3), x, x are factors of the term (–3x²); 2 is the factor of the term 2.
• The terms and factors of the terms of an expression can be represented by a tree diagram. The tree diagram for the expression 2xy – 3x² +2 can be represented as follows:
 
 
❖ The numerical factor of a term is known as its coefficient. For example, for the term –3x²y, the coefficient is (–3).
❖ The terms having the same algebraic factors are called like terms, while the terms having different algebraic factors are called unlike terms.
    For example: 13x²y, – 23x²y are like terms; 12xy, 3x² are unlike terms.

❖ Expressions can be classified on the basis of the number of terms present in them.
• Expression containing only one term is called a monomial.
  Example: 2x, –3x², 2xy, etc.
• Expression containing only two unlike terms is called a binomial. 
  Example: 2x + 3, 3x² – 2, – 2xy + 3y², etc.
• Expression with three terms, where the terms are unlike, is called a trinomial.
  Example: 2x² –3x + 1, – 2xy + 5y + 6x, etc.

In general, the expression with one or more terms is called a polynomial.
❖ Addition and subtraction of algebraic expressions
• The sum or difference of two like terms is a like term, with its numerical coefficient equal to the sum or difference of the numerical coefficients of the two like terms.
• When algebraic expressions are added, the like terms are added and unlike terms are left as they were.

❖ Value of an expression at given values of variables
• The value of an expression depends on the values of the variables forming the expression.
• The value of an expression at particular values of variables can be found by substituting the variables by the corresponding values given.

❖ Rules and formulas are written in general form by using algebraic expressions.       
    For example: Area of a square of side s is s².
 
❖ Certain number patterns can also be written in general form by using expressions.
    For example, 9, 19, 29 ….
   Here, 9 = 10 – 1, 19 = 10 × 2 – 1, 29 = 10 × 3 – 1; therefore, this pattern can be written in general form as (10n – 1), where n is the number of terms.Chapter 13: Exponents and Powers
 
❖ We use exponents to write very large numbers.
For example, 1000000000 can be written as 10 × 10 × 10 × 10 ×10 × 10 × 10 × 10 × 10 = 10⁹
It is read as ten raised to the power nine, where 10 is known as base and 9 as the exponent.
The number 10⁹ is known as exponential form of 1000000000.
 
❖ Laws of exponents
• $a^m\times a^n=a^{m+n}$
•  $a^m÷a^n=a^{m-n}$
•  ${\left(a^m\right)}^n=a^{mn}$
•  $a^m \times b^m={\left(ab\right)}^m$
•
Example: Solve (i) 2⁷ × 2³ (ii) 3⁴ ÷ 3⁵ (iii) (5²)³  (iv) 2³ × 5³

Solution:
(i) 2⁷ × 2³ = 2⁷⁺³ = 2¹⁰
(ii) 3⁴ ÷ 3⁵ = 3^4–5 = 3^–1
(iii) ${\left(5^2\right)}^3=5^{2\times 3}=5^6$
(iv) $2^3\times 5^3={\left(2\times 5\right)}^3 ={10}^3$
 
❖ Any number with exponent 0 is equal to 1, that is, 2⁰ = 3⁰ = (–1)⁰ = 1

❖ (–1)^{even number}  = 1 and (–1)^{odd number}  = –1

❖ The numbers can be written in the expanded form using exponents.
     For example: 48067 = 4 × 10000 × 8 × 1000 + 0 × 100 + 6 × 10 + 7
                                      = 4 × 10⁴ + 8 × 10³ + 0 × 10² + 6 × 10¹ + 7 × 10⁰

❖ All numbers can be written in the exponential form by expressing them as a decimal number between 1.0 and 10.0, multiplied by a power of 10
    For example:
    7 = 7.0 × 10⁰
    5347 = 5.347 × 10³Chapter 14: Symmetry

❖ The line of symmetry of a figure is a line dividing the figure into two halves in such a way that the two halves will coincide if the figure is folded alone the line.

❖ Line of symmetry of regular polygons
• A polygon is said to be regular if all its sides are equal and all its interior angles are of equal measure.
   For example: Equilateral triangle, Square
• A regular polygon has as many lines of symmetry as its number of sides.
  (i) An equilateral triangle has three lines of symmetry.
  (ii) A square has four lines of symmetry.

❖ Rotational symmetry
• Rotation means turning of an object about a fixed point.
• The fixed point is known as the centre of rotation.
• The angle of turning during the rotation is called the angle of rotation.
• If an object looks exactly the same after rotation, it is said to have rotational symmetry.
• A complete rotation means a rotation of 360°.
• In a complete rotation, the number of times an object looks exactly the same is known as the order of rotational symmetry.
  For example: Consider the rotation of the following floral design.
 
 
 Here, the angle of rotation is 90° and in a full turn, there are precisely four positions when the figure looks exactly the same. Therefore, it has a rotational symmetry of order four.
 
❖ Some shapes or figures have only lines of symmetry, some have only rotational symmetry and some have both symmetries.Chapter 15: Visualising Solid Shapes
 
❖ Plane figures like rectangle, square, etc., are two-dimensional figures.
❖ Solid shapes like sphere, cylinder, cuboid, etc., are three-dimensional figures.
❖ The corners of a solid figure are called its vertices; the line segments joining the vertices are known as its edges; and its flat surfaces are called faces.
❖ A net is a skeleton outline of a solid, which can be folded to make the solid.
    For example:
   
 
❖ Oblique sketches
• Oblique sketches are drawn on squared (lines or dots) paper.
• In oblique sketches, the lengths of the sides are not proportional to the actual solid.
  For example: The given figure shows a cube of dimensions 3 units.
  
 
❖ Isometric sketches
• Isometric sketches are drawn on isometric dot paper.
• In isometric sketches, the lengths are proportional to the actual solid.
  For example: The given figure represents a cuboid of dimensions 4 units × 3 units × 2 units.

 
 
❖ Visualising three-dimensional figures from different views
  
The given solid when viewed from the given directions gives
 
 as the front view
 
  as the top view
 
as the side view