Series combination

In a series connection, all resistors are connected end to end (lengthwise) with each other. In such connections, the total resistance of the circuit increases. The given figure shows three resistors of resistance R1, R2, and R3 respectively connected in a series with each other.
The equivalent resistance of the resistors connected in series is given by the algebraic sum of their individual resistances.
Equivalent resistance or RS = R1 + R2 + R3
derivation of it :
Suppose, there are ‘n’ resistances connected in series. The resistances are: R 1 , R 2 , R 3 , R 4 …… R n . Voltage ‘V’ is applied across the ends of the connection. Let I current flown through the series of resistances.
Since, current I will be same through all the resistances and the sum of voltage drop across all the resistances gives us the voltage ‘V’. Therefore,
V = IR 1 + IR 2 + IR 3 + IR 4 +………….. IR n
=> V = I(R 1 + R 2 + R 3 + R 4 +………….. R n )
Thus, the series of resistances can be summed up and the equivalent resistance of the circuit is the sum of the resistances.
Therefore, V = IR s
Where, R s = R 1 + R 2 + R 3 + R 4 +………….. R n
Parallel combination
Here three resistances are connected in parallel.In this case the potential difference across the ends of all the resistances will be same and it will be equal to the voltage of the battery used.

Suppose the total current flowing through the circuit=I,then the current passing through resistance 
Current through  and current through
and current through 

power :
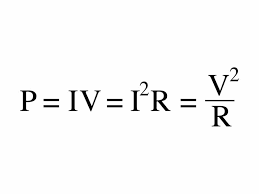
Electrical Energy is E = P × t





 and current through
and current through 
