- Two sides and the included angle are congruent
- AC = ZX (side)
-
ACB = XZY (angle) - CB = ZY (side)
- Therefore, by the Side Angle Side postulate, the triangles are congruent.
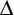ABC 
XYZ 
If we can prove SAS congruence by this method, why can't we prove ASA congruence by this ?
We can take two triangles ABC and DEF with angle A = angle D, angle B = angle E and side AB = DE ..!
Then we can simply put triangle DEF over triangle ABC and we'll see that all its corresponding parts will coincide which indeed proves that both the triangles are congruent. Thus equal in area.
I just want to know why can't we prove ASA congruence by this method ?
Please answer it as soon as possible.
The mentioned is not the proof of SAS but rather simply statements through which we are proving two triangles i.e., ΔABC and ΔXYZ to be congruent using SAS congruency criterion.
Here is the proof of ASA congruency criterion i.e., "two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle."
Given: Two ΔsABC and DEF such that
∠B = ∠E, ∠C = ∠F and BC = EF
To Prove: 
Proof: There are three possibilities.
CASE I: When AB = DE,
In this case, we have
AB = DE
∠B = ∠E [Given]
and, BC = EF [Given]
So, by SAS criterion of congruence, .
CASE II: When AB < ED
In this case take a point G on ED such that EG = AB. Join GF.
Now, in ΔsABC and GEF, we have
AB = GE [By supposition]
∠B = ∠E [Given]
and, BC = EF [Given]
So, by SAS criterion of congruence
⇒ ∠ACB = ∠GFE [
Corresponding parts of congruent triangles are equal]
But ∠ACB = ∠DFE [Given]
∴ ∠GFE = ∠DFE
This is possible only when ray FG coincides with ray FD or G coincides with D.
Thus, in ΔsABC and DEF, we have
AB = DE [As proved above]
∠B = ∠E [Given]
and, BC = EF [Given]
So, by SAS criterion of congruent,
CASE III: When AB > ED.
In this case take a point G on ED produced such that EG = AB. Join GF. Now, proceeding exactly on the same lines as in case II, we can prove that
Hence,