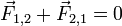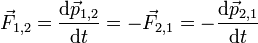the force which when appied on a body of mass of 1kg provides the acceleration of 1m/s2 is known as 1 newton force.
1 newton foce = 1kg m/s2.
- 83
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces. They have been expressed in several different ways over nearly three centuries, and can be summarized as follows:
- First law: The velocity of a body remains constant unless the body is acted upon by an external force.
- Second law: The acceleration a of a body is parallel and directly proportional to the net force F and inversely proportional to the mass m, i.e., F = m a.
- Third law: The mutual forces of action and reaction between two bodies are equal, opposite and collinear.
- 3
The newton (symbol: N) is the SI derived unit of force, named after Isaac Newton in recognition of his work on classical mechanics.
- 16
Heyyyy.....here is ur answer :---
Newton's First Law of Motion:
I. Every object in a state of uniform motion tends to remain in that state of motion unless an external force is applied to it.It is also known as law of inertia.....Newton's Second Law of Motion:
II. The relationship between an object's mass m, its acceleration a, and the applied force F is F = ma. Acceleration and force are vectors, in this law the direction of the force vector is the same as the direction of the acceleration vector......This is the most powerful of Newton's three Laws, because it allows quantitative calculations of dynamics: how do velocities change when forces are applied. Notice the fundamental difference between Newton's 2nd Law and the dynamics of Aristotle: according to Newton, a force causes only a change in velocity (an acceleration) it does not maintain the velocity as Aristotle held......
Newton's Third Law of Motion:
III. For every action there is an equal and opposite reaction.This law is exemplified by what happens if we step off a boat onto the bank of a lake: as we move in the direction of the shore, the boat tends to move in the opposite direction (leaving us face down in the water, if we aren't careful!)......
Hopezzz......, u understand ir now,
So, cheerzzzz....... :-D
And thumbzzzz.....up plzzz......!!!!! :-)
- -4
the three laws r
- -5
Newton's Third Law is a result of applying symmetry to situations where forces can be attributed to the presence of different objects. The third law means that all forces are interactions between different bodies, and thus that there is no such thing as a unidirectional force or a force that acts on only one body. Whenever a first body exerts a force F on a second body, the second body exerts a force −F on the first body. F and −F are equal in magnitude and opposite in direction. This law is sometimes referred to as theaction-reaction law, with F called the "action" and −F the "reaction". The action and the reaction are simultaneous:
If object 1 and object 2 are considered to be in the same system, then the net force on the system due to the interactions between objects 1 and 2 is zero since
This means that in a closed system of particles, there are no internal forces that are unbalanced. That is, the action-reaction force shared between any two objects in a closed system will not cause the center of mass of the system to accelerate. The constituent objects only accelerate with respect to each other, the system itself remains unaccelerated. Alternatively, if an external force acts on the system, then the center of mass will experience an acceleration proportional to the magnitude of the external force divided by the mass of the system.
Combining Newton's Second and Third Laws, it is possible to show that the linear momentum of a system is conserved. Using
and integrating with respect to time, the equation:
is obtained. For a system which includes objects 1 and 2,
which is the conservation of linear momentum.[18] Using the similar arguments, it is possible to generalize this to a system of an arbitrary number of particles. This shows that exchanging momentum between constituent objects will not affect the net momentum of a system. In general, as long as all forces are due to the interaction of objects with mass, it is possible to define a system such that net momentum is never lost nor gained
- 8