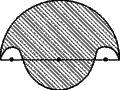
The boundary of the shaded region in the figure given consists of four semi-circular arcs, the smallest two being equal. If the diameter of the larger is 14 cm and of the smallest is 3·5 cm, calculate the length of the boundary and the area of the shaded region. (Take ![]() = 22/7).
= 22/7).

In the given figure, PS = 14 cm is a diameter of a circle and PQ = 3.5 cm
The length of PQ and RS are equal,
So,
![]()
![]()
So, radius of semicircle RMSR = radius of the semicircle PBQP
![]()
And radius of semicircle QERQ,
![]()
And radius of the semicircle PTSP,
![]()
The length of the boundary = 2×Perimeter of the semicircle PBQP![]() Perimeter of the semicircle PTSP
Perimeter of the semicircle PTSP![]() Perimeter of the semicircle QERQ
Perimeter of the semicircle QERQ

Hence the length of the boundary will be 44 cm.
Now,
Area of the shaded region = Area of the semicircle PTSP![]() 2×Area of the semicircle PBQP+ Area of the semicircle QESQ
2×Area of the semicircle PBQP+ Area of the semicircle QESQ

Hence area of the shaded region will be 86.546 cm2.

