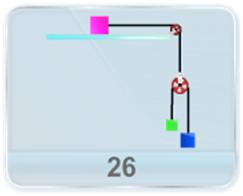
Three blocks of masses m1, m2 and m3 are connected as shown in figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
hi Atul Tripathi ,
Please find below the solution to the asked query:

as we can see in the diagram:
let us say the tension in the string attached to m1 be T1 and the tension in the string attached to m2 and m3 be T2
Let us say the acceleration of m1 be a1 and the acceleration of m2 be a2 while the acceleration of m3 be a3.
If you have any more doubts just ask here on the forum and our experts will try to help you out as soon as possible.
Please find below the solution to the asked query:

as we can see in the diagram:
let us say the tension in the string attached to m1 be T1 and the tension in the string attached to m2 and m3 be T2
Let us say the acceleration of m1 be a1 and the acceleration of m2 be a2 while the acceleration of m3 be a3.
If you have any more doubts just ask here on the forum and our experts will try to help you out as soon as possible.

